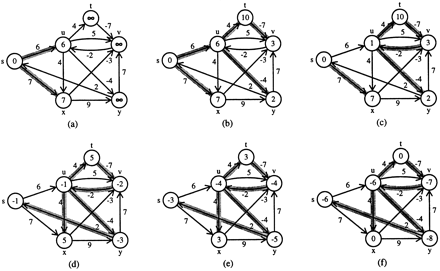
So as to demonstrate how the standard Bellman–Ford algorithm fails when inconsistent subsystems exist, one vertex and two edges are added to the previously solvable difference system. This difference system contains two negative cycles, which prevent the Bellman–Ford algorithm from solving the single-source shortest path problem. Our display method is identical to that used in Fig. 4, with the exception that the initial upper bounds (∞) are not shown. Instead, a depicts the state of the graph after the first pass of relaxation steps. Notice that after c, at which point s is no longer the root of the predecessor tree, the upper bounds for the variables u,v, and t continue to decrease. And after this point, any relaxation of one of the edges joining these vertices continues to lower the shortest path estimates without a lower bound in sight.











