Modeling Human Evolution—To Tree or Not to Tree?
Underhill et al. (this issue) report 19 new Y chromosome markers from a survey of 718 human genomes and use these data to construct a gene genealogy. According to the data, most of these biallelic markers were restricted to a few populations in specific regions of the world, but a few occurred at varying frequencies in all populations sampled, implying that they are older mutations. Underhill and colleagues constructed a genealogy of these polymorphisms using a novel combination of parsimony methodology and marker frequencies in 10 extant regional samples. In the discussion that follows, we distinguish the separate histories of chromosomal regions, individuals, and populations, as the interpretation of the branching process implied by a tree-like relationship between descendant nodes (the point at which branching occurs) becomes less clear as the level of analysis moves from chemical residues to aggregate populations. A clearer understanding of aggregate population structure and history may also be obtained using other conventional methods that do not impose a bifurcating process on the data. We illustrate one such method by reanalyzing the data reported by Underhill et al. (this issue) with principal components and plotting the principal coordinates of the populations (Cavalli-Sforza et al. 1994).
General Issues and Methods in Phylogenetic Inference
The branching pattern or topology of a network provides a graphical description of the mutation process that differentiates chromosomal haplotypes, provided that reversions of mutations to the ancestral states are rare. When the ancestral states of the mutations have been determined, networks may be rooted in a time dimension and are then considered trees. Trees can be constructed from either discrete character data or frequency data, and in either case the primary concerns are whether the topology and branch lengths are correct. Numerous tree-building methods have been proposed (e.g.,Sneath and Sokal 1973; Nei 1987; Felsenstein 1988), and excellent discussions of method performance are available (e.g., Sober 1988;Cavalli-Sforza et al. 1994; Nei 1996; Li 1997). Because no single approach works well in all circumstances the method of choice is often a matter of personal preference and the constraints of the data. The most popular methods can be classified into three broad categories: (1) character state analysis; (2) distanced-based analysis; and (3) maximum likelihood analysis. Each category is discussed briefly in turn and is followed by analyzing the data of Underhill et al. (this issue) by an alternative statistical method.
Character State Analysis
In character state analysis, the states of the ancestral markers are inferred from extant samples, and a tree is produced by minimizing the number of overall marker state changes (mutations) in the tree using the criteria of maximum parsimony (MP) (Farris 1972). The MP algorithm searches for the tree that requires the fewest total number of mutational changes to explain the variation in the observed taxa. Often several trees of the same minimal length can be obtained, and in these cases no unique tree can be inferred. Additionally, when the degree of divergence between taxa is large, parallel and reverse mutations may become sufficiently frequent to cause the method to fail (Felsenstein 1978).
The MP tree topology reported in Underhill et al. (this issue, Fig. 2) was constructed under the standard assumption of minimal reversion mutations, and the root was placed by typing each marker for its ancestral state in a nonhuman primate. The investigators’ use of gene frequencies to infer the times of origin of each mutation, while based on standard theories of stochastic substitution processes, is appropriate only under their assumption of nonrecurrent mutation and their inference of the ancestral state. If multiple changes are possible at a site, then very old markers, once possibly fixed or at high frequency in the population but fated for extinction in the near future, could be sampled at low frequency in extant populations and mistaken for much younger mutations. However, given the simple observed pattern of substitutions, such a scenario is unlikely for the present data.
Distance-Based Analysis
In contrast to character state methods, which group taxa based on the number of shared marker states, distance-based methods define the similarity between taxa by transforming the raw data into a single measure of evolutionary distance. Evolutionary distances are computed for all pairs of taxa, and a network is constructed by using an algorithm based on some functional relationships among the distance values. The two most popular distance-based methods are the unweighted pair group method with arithmetic mean (UPGMA) and neighbor joining (NJ).
The UPGMA (Sokal and Michener 1958) is the simplest method for tree reconstruction and assumes that rates of evolutionary change (mutation) are equal across time for all lineages. This assumption is violated frequently by real data, and, as a result, an inferred UPEMA tree often involves topological errors (Saitou and Nei 1987).
The NJ method (Saitou and Nei 1987) groups taxa as neighbors in a sequence that minimizes the total length of the tree. The method, unlike UPGMA, produces an unrooted network. Rooting is obtained with additional information (such as an outgroup taxon) or additional assumptions (midpoint averaging). The performance of NJ, like other distance-based methods, is affected by the accuracy of the estimated distances between taxa (Li 1997). The performance of the algorithm may be compromised when sequences are short, distances are large, or if the mutation rate varies greatly across markers (Li 1997).
Maximum Likelihood Analysis
The final broad category is maximum likelihood (ML) analysis (Felsenstein 1981). In this method, ML values for marker state configurations (pattern of marker differences at each locus over all taxa) are computed for each possible tree, and the algorithm selects the configuration with the largest value as the preferred tree. In the past, ML was used infrequently because of the large computational demands of the algorithm, but with the advent of more powerful computers, interest has expanded in this method (Hasegawa et al. 1985;Felsenstein 1988; Saitou 1988; Strimmer and von Haeseler 1996).
Although gene genealogies constructed by any of the above methods can provide a clear picture of the evolutionary history of the nonrecombining chromosomal segment investigated by Underhill et al. (this issue), care must be exercised in inferring the history of a population from such a graph (Nei 1987). It has been shown that migration can mimic branching histories and vice versa (Felsenstein 1982), and groups of unequal size can distort our inferences of genetic distance analysis (Relethford and Harpending 1995). In the following section we present an analysis of the Underhill et al. (this issue)data using a conventional statistical technique to evaluate the historical inferences made by these investigators.
Principal Component Analysis
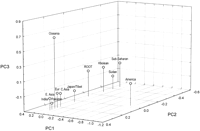
Principal component (PC) analysis and related methods like principal coordinate analysis, multidimensional analysis, and factor analysis are procedures for condensing multivariate data into fewer variables with a minimum loss of information (Cavalli-Sforza et al. 1994). PC analysis is a useful complement to tree construction when frequency data are being considered (Cappello et al. 1996; Harpending et al. 1996; Stoneking et al. 1997), as it, unlike a tree, does not impose a history of bifurcations on contemporary population structure. Rather, a PC genetic map shows evolutionary distance between populations as Euclidean distance in two or three dimensions, as illustrated here (Fig. 1) with a map of the Underhill et al. (this issue) data that capture 61% of the variation in the 20 haplotypes.
PC plot of biallelic Y chromosome polymorphisms by geographic region. The first three PCs of the Underhill et al. (this issue) data set plotted as PCs for 10 regional populations. This three-dimensional projection captures 61% of the variation present in the 20 haplotypes reported in the study. The root was placed by introducing a hypothetical population with a 100% frequency for the ancestral A1 haplotype into the analysis.
The first PC separates the New World and Old World populations because of the high frequency and restricted distribution of haplotype C7. The second PC separates African and non-African populations in a very linear manner, and the third PC separates the Sahulian populations of Oceania from a dense cluster of Eurasian groups because of the restricted distribution of haplotypes C3, C4, and C5. The root was included by adding a hypothetical population fixed for haplotype A1 to the analysis. In this three-dimensional projection it is centrally placed between the African and Eurasian population clusters. The pattern of population clustering observed from the Y-specific biallelic markers reported by Underhill et al. (this issue) is similar to patterns observed for nuclear β-globin gene sequence (Harding et al. 1997) and polymophic Alu insertion frequency data (Stoneking et al. 1997).
The consistency between the population clusters revealed in the PC analysis and the gene genealogy reported by Underhill et al. (this issue) from the same set of data, and the larger consistency between these Y chromosome results and previous genetic studies, lends confidence to collective inferences about contemporary human population structure and evolutionary history.
Footnotes
-
↵1 Corresponding author.
-
E-MAIL mbatze{at}lsumc.edu; FAX (504) 568-6037.
- Cold Spring Harbor Laboratory Press