Artificial intelligence and machine learning in cell-free-DNA-based diagnostics

  1. Y.M. Dennis Lo1,2,3,4
  1. 1Center for Novostics, Hong Kong Science Park, Pak Shek Kok, New Territories, Hong Kong SAR, China;
  2. 2Li Ka Shing Institute of Health Sciences, The Chinese University of Hong Kong, Shatin, New Territories, Hong Kong SAR, China;
  3. 3Department of Chemical Pathology, The Chinese University of Hong Kong, Shatin, New Territories, Hong Kong SAR, China;
  4. 4State Key Laboratory of Translational Oncology, The Chinese University of Hong Kong, Shatin, New Territories, Hong Kong SAR, China
  • Corresponding author: loym{at}cuhk.edu.hk
    •  
    Next Section

    Abstract

    The discovery of circulating fetal and tumor cell-free DNA (cfDNA) molecules in plasma has opened up tremendous opportunities in noninvasive diagnostics such as the detection of fetal chromosomal aneuploidies and cancers and in posttransplantation monitoring. The advent of high-throughput sequencing technologies makes it possible to scrutinize the characteristics of cfDNA molecules, opening up the fields of cfDNA genetics, epigenetics, transcriptomics, and fragmentomics, providing a plethora of biomarkers. Machine learning (ML) and/or artificial intelligence (AI) technologies that are known for their ability to integrate high-dimensional features have recently been applied to the field of liquid biopsy. In this review, we highlight various AI and ML approaches in cfDNA-based diagnostics. We first introduce the biology of cell-free DNA and basic concepts of ML and AI technologies. We then discuss selected examples of ML- or AI-based applications in noninvasive prenatal testing and cancer liquid biopsy. These applications include the deduction of fetal DNA fraction, plasma DNA tissue mapping, and cancer detection and localization. Finally, we offer perspectives on the future direction of using ML and AI technologies to leverage cfDNA fragmentation patterns in terms of methylomic and transcriptional investigations.

    Previous SectionNext Section

    The biology of cell-free DNA

    Cell-free DNA (cfDNA) represents fragmented DNA molecules in the bloodstream, urine, saliva, or other bodily fluids but not encapsulated within cells. Many studies focus on circulating plasma DNA, unveiling a number of important biological features such as its tissues of origin and characteristic fragmentation patterns (Lo et al. 2021). Early interest in cfDNA was driven by the identification of circulating tumor DNA (ctDNA) in the plasma of cancer patients (Stroun et al. 1989; Nawroz et al. 1996), offering a means of noninvasive cancer detection and design of targeted therapy (Kwapisz 2017). A parallel development is the discovery of fetal DNA in the maternal plasma (Lo et al. 1997), opening up possibilities in noninvasive prenatal testing (NIPT), especially in the prenatal screening of fetal chromosomal aneuploidies (Chiu et al. 2008, 2011). Subsequently, the identification of donor-derived DNA in the plasma of organ transplant recipients (Lo et al. 1998a) has sparked interest in noninvasive approaches for monitoring organ rejection (De Vlaminck et al. 2014; Schütz et al. 2017; Keller and Agbor-Enoh 2021; Khush et al. 2021; Bu et al. 2022; Cheng et al. 2022; Keller et al. 2024).

    Several mechanisms for cfDNA release have been proposed, such as apoptosis, necrosis, and NETosis, or active cellular secretion (Grabuschnig et al. 2020; Han and Lo 2021), but their relative involvement in the shedding of cfDNA into plasma remains unclear. On the other hand, exciting progress has been made on cfDNA fragmentation processes, and a number of fragmentomics markers have been developed (Han et al. 2020; Lo et al. 2021). It is known that human plasma DNA shows a modal length of ∼166 bp, reflecting the length of DNA associated with a nucleosome plus linker. Fetal- and tumor-derived cfDNA molecules exhibit a shorter modal size of ∼143 bp (Lo et al. 2010; Chandrananda et al. 2015), opening up possibilities for size-based enrichment of fetal and tumoral signals. Fragments <143 bp exhibit a 10 bp size periodicity (Lo et al. 2010; Mouliere et al. 2018), which provides a mechanistic link between cfDNA fragmentation and nuclease-mediated cleavages acting on the exposed groove of the nucleosome-bound DNA double helix (Noll 1974). Indeed, many studies suggest that a proportion of cfDNA molecules circulate in the bloodstream as cell-free nucleosomes (Sadeh et al. 2021; Fedyuk et al. 2023). Interestingly, the levels of these circulating nucleosomes and their posttranslational histone modifications differ in the plasma of individuals with cancer compared with those without, as well as across different cancer types (Sadeh et al. 2021; Fedyuk et al. 2023).

    There is evidence that the fragmentation patterns at the ends of cfDNA fragments are nonrandom. In particular, the distributions of nucleotides at cfDNA ends are not uniform across all possible permutations (Serpas et al. 2019). Currently, these patterns in end motifs are believed to be partly caused by the action of nucleases, such as deoxyribonuclease 1 (DNASE1), deoxyribonuclease 1L3 (DNASE1L3), and DNA fragmentation factor subunit beta (DFFB) (Han and Lo 2021). It is known that nucleases like DFFB and DNASE1L3 play important roles in apoptotic DNA fragmentation (Widlak and Garrard 2009; Mizuta et al. 2013; Keyel 2017). Some nucleases, like DNASE1L3 and DNASE1, show tissue-specific patterns of expression (Keyel 2017). Furthermore, secreted DNASE1L3 and DNASE1 are believed to be major contributors to serum DNase activity (Napirei et al. 2009), which may be important for the clearance of serum DNA/chromatin complexes (Sisirak et al. 2016). Indeed, loss of function in Dnase1l3 or Dnase1 is associated with systemic lupus erythematosus (SLE) in humans and mice (Napirei et al. 2000; Al-Mayouf et al. 2011).

    Using genetically modified mice in which one or more nuclease genes had been knocked out, the action of individual nucleases could be studied (Serpas et al. 2019; Han et al. 2020; Chen et al. 2022a). Mice with homozygous Dnase1 deletion exhibited no obvious alteration in overall fragment length distribution. However, when the Dnase1l3 gene was knocked out, there was an increase in the proportions of di- and trinucleosomal plasma DNA molecules (Serpas et al. 2019). Additionally, the relative frequencies of specific four-base motifs at the 5′ ends of plasma DNA fragments were significantly perturbed in Dnase1l3 knockout mice, in which the six most decreased end motifs all began with “CC” (Serpas et al. 2019). Therefore, DNASE1L3 likely contributes to the generation of fragments with CC-ends in plasma. Extending this work, Han and colleagues (2020) demonstrated the distinct roles of DNASE1, DNASE1L3, and DFFB on cfDNA cleavage by studying cfDNA fragmentation in plasma samples undergoing in vitro incubation in the presence of heparin or EDTA, showing that DNASE1 and DFFB preferentially generate T-end and A-end fragments, respectively. Apart from patterns in nucleotide composition, nuclease activity has also been shown to be associated with the recently discovered single-stranded overhangs on dsDNA, known as jagged ends (Jiang et al. 2020b; Ding et al. 2022).

    The involvement of various DNA nucleases in cfDNA fragmentation could retrospectively explain, in part, the observation that the ends of cfDNA fragments preferentially occurred at certain genomic coordinates, referred to as “preferred ends” (Chan et al. 2016; Jiang et al. 2018). Differential patterns of preferred ends were described between the maternal and fetal genomes (Chan et al. 2016), as well as between the tumor and nontumor genomes (Jiang et al. 2018). This unevenness of genome-wide fragmentation patterns has also been parameterized in the “window protection score” for nucleosome footprinting (Snyder et al. 2016; Straver et al. 2016). Together, these studies highlight that patterns of cfDNA fragmentation are intimately linked to chromatin architecture, such as nucleosome arrays, sites of other DNA-binding proteins (e.g., CCCTC-binding factor [CTCF]), and open chromatin regions that are associated with transcriptional activity.

    As cfDNA molecules exhibiting these characteristic fragmentation patterns can be shed from different tissues into the circulation, it is diagnostically useful to dissect the tissues of origin of cfDNA. In this regard, many studies have demonstrated that methylation analysis of plasma cfDNA allows tissue-of-origin tracing of cfDNA in plasma (Luo et al. 2021; Oberhofer et al. 2022). These studies reveal that cfDNA is derived from a variety of tissues and cell types in which the major contributor is hematopoietic cells, whereas other solid tissues such as the liver also have appreciable contributions (Sun et al. 2015; Moss et al. 2018). Furthermore, tissue-of-origin analyses can serve to pinpoint the site of pathology (Sun et al. 2015; Kang et al. 2017; Moss et al. 2018) and determine the tissue origin of cancers of unknown primary (Conway et al. 2024). Recently, the compilation of a high-resolution human methylome atlas consisting of 39 cell types sorted from 205 healthy tissue samples (Loyfer et al. 2023) has provided a valuable resource for developing tissue-specific methylation biomarkers for future tissue-of-origin studies.

    Taken together, many methylomic and fragmentomic features of cfDNA molecules have recently come into the spotlight, promising to expand our knowledge of cfDNA biology and their clinical applications. Advancements in analytical and bioinformatic tools based on artificial intelligence (AI) and machine learning (ML) can exploit these features holistically to augment the performance of cfDNA-based diagnostics (Fig. 1). In this review, we particularly elaborate on AI and ML technologies that are applied in cfDNA-based diagnostics, such as noninvasive prenatal testing and cancer detection.

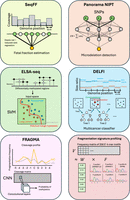
    Figure 1.
    View larger version:
    Figure 1.

    ML algorithms exploit cfDNA features for applications in NIPT, cancer liquid biopsies, and emerging areas of cfDNA biology. (Upper left) SeqFF uses elastic net to process local coverage in 50 kb genome-wide bins for fetal fraction estimation. (Upper right) Natera uses DNN to process linkage information between SNPs for microdeletion detection. (Middle left) SVM was used to detect lung cancer using the methylation status of selected differentially methylated regions (DMRs). (Middle right) The DELFI algorithm feeds local size and coverage profiles into a gradient boosting model to achieve multicancer detection. (Lower left) In one implementation of FRAGMA, a CNN is used to analyze the cleavage around a differentially methylated CpG site to determine CpG methylation status. (Lower right) NMF deconvolution of the frequencies of 256 5′ 4-mer end motifs yields “founder” profiles of potential biological significance.

    Previous SectionNext Section

    Introduction of AI and ML

    AI and ML are now commonly used interchangeably to refer to computer-based models that identify meaningful patterns in a bulk of information to build classification and prediction models based on training data. However, the meaning of AI and ML has shifted over time, and so, it is notoriously difficult to define these two terms (Hoffmann 2022). Historically, AI was proposed by Alan Turing as the capacity for a machine to “think” in such a way that a human cannot, in blinded conversation, distinguish between the machine and a real human (Turing 1950; Muggleton 2014; Wooldridge 2021). According to Turing, the behavior of such a machine would most likely be learned from data that were provided externally (Turing 1950). This process is now called machine learning (ML), for which many algorithms have been developed to perform different functions (Table 1). Many authors thus define ML as a subdiscipline of AI (Alloghani et al. 2020; Mueller and Massaron 2021; Hoffmann 2022).

    View this table:
    Table 1.

    A list of common supervised and unsupervised ML/AI algorithms

    The theoretical basis for AI was proposed in the 1940s–1950s (McCulloch and Pitts 1943; Rosenblatt 1958), which involved modeling the activity of a small number of neurons. However, these simple models were far from being able to simulate the more complex behavior needed for tasks above just arithmetic, let alone truly intelligent behavior (Wooldridge 2021). The explosive increase of computational power in the twenty-first century enabled deep learning, which uses “deep” neural networks (DNNs), to be applied widely (Hoffmann 2022). Because of the analogies to neuronal mechanics in the brain, deep learning is now commonly referred to as AI-based technologies. In contrast, ML is now more generally used to describe other types of classifiers (such as support vector machines [SVMs]) or regressors. We shall henceforth use “ML” as a general term covering both classical ML and deep learning and shall use “AI” to refer specifically to deep learning.

    ML can be primarily divided into three types according to the desired outcomes: classification, clustering, and regression. Both classification and regression are considered “supervised” learning, for which the model parameters are established based on samples with known class labels (Alloghani et al. 2020). Classification models return categorical variables as the final output (e.g., a pregnancy involving a normal or trisomic fetus), whereas regression models return continuous variables (e.g., fetal DNA fraction in maternal plasma). On the other hand, unsupervised learning is when the analysis is performed without relevant labels, such as in clustering algorithms that organize data into subgroups. Both classical and AI-based supervised and unsupervised learning (Table 1) have been applied in a wide range of studies, including fragmentomic-based cancer detection (Cristiano et al. 2019; Jiang et al. 2020a), cfDNA tissue-of-origin deconvolution (Li et al. 2023b), and direct methylation analysis in single-molecule real-time (SMRT) sequencing (Tse et al. 2021).

    An essential component in ML is to find the best model parameters that achieve the desired performance of classification or regression through iterative optimization (Sun et al. 2020; Greener et al. 2022). The difference between predictions from the model and the actual values is parameterized by a loss function, so that a lower value of the loss function indicates better model performance (Ciampiconi et al. 2023). Hence, the main goal of optimization algorithms such as gradient descent is to iteratively adjust the model parameters to minimize the loss function. Gradient descent calculates the gradient of the loss function and iteratively updates the parameters in the opposite direction of the gradient, thus finding a local minimum. The design of the loss function directly affects the model function (Efron and Hastie 2016; Ciampiconi et al. 2023): For example, LASSO regression adds an L1-penalty term to the loss function, which has the effect of pruning less informative features from the model, and so essentially performs feature selection alongside the main regression task.

    Deep learning

    Recently, deep learning–based AI technologies have been introduced into genomic data analysis. Deep learning is based on DNNs, which are constructed from multiple layers of interconnected neurons. Fundamentally, each “neuron” is a function that takes in multiple weighted inputs and a bias to compute an output, which is then sent to the next neuronal layer (McCulloch and Pitts 1943; Rosenblatt 1958). The bias in a neuron is defined as a constant that is added to the product of input features and weights. This bias can tune the response of the neuron (such as its activation threshold) to various input conditions, making the neural network more robust and capable of handling complex patterns. The resulting network is able to perform complex tasks because many simple operations are carried out in a massively parallel manner (Bishop 1995). Compared with the commonly used ML algorithms mentioned above, the number of optimizable parameters—weights and biases—in a DNN is often much larger than the number of input features. For example, if a DNN takes 10 initial inputs, two hidden layers of five and four neurons each, and an output layer of three neurons, the number of weights is (10 × 5) + (5 × 4) + (4 × 3) = 82; the number of biases is 5 + 4 + 3 = 12; and so, the total number of parameters in such a DNN is 82 + 12 = 94. In comparison, the number of parameters in a logistic regression (in this case, the coefficients) is equal to the number of input features: A logistic regression model with 10 features would have 10 parameters under training. More optimizable parameters in DNNs usually lead to better performance than the aforementioned classical ML algorithms, given that a sufficient number of training samples is used to train the model. A widely used rule of thumb is that the number of training data points should be 10 times the number of weights (Abu-Mostafa et al. 2012), but some authors have suggested a more conservative minimum ratio of 50 (Alwosheel et al. 2018). Thus, it is crucial that the training data set is sufficiently large to prevent data sparsity, and so DNNs cannot be appropriately applied to situations in which the number of training samples is lacking.

    An example of AI-based approaches is direct methylation analysis using SMRT sequencing (Tse et al. 2021). 5-Methylcytosine (5mC) is the most common base modification, which plays important roles in genomic imprinting, X-Chromosome inactivation, and carcinogenesis (Smith and Meissner 2013). 5mC is classically detected using bisulfite sequencing (BS-seq), but BS-seq is destructive and reduces sequence complexity. BS-seq itself also cannot distinguish 5mC from 5-hydroxymethylcytosine (5hmC), which requires multiple enzymatic and chemical reactions to differentiate them, such as oxidation by 10–11 translocation enzymes (Hahn et al. 2015). On the other hand, “third-generation” sequencing such as SMRT or nanopore sequencing reads DNA directly. In SMRT sequencing, a DNA polymerase incorporates fluorescent nucleotides into the newly synthesized strand, and the kinetics of nucleotide incorporation (inter-pulse duration [IPD], and pulse width [PW]) are affected by base modifications. However, the difference in kinetics between C and 5mC is extremely subtle in SMRT sequencing, leading to challenges in methylation calling, and thus, many attempts have failed to achieve meaningful or practical accuracy for a decade (Clark et al. 2013). Tse and colleagues (2021) have developed an AI-based approach named the holistic kinetic (HK) model (Fig. 2), which takes into account the incorporation of kinetics and sequence context for every nucleotide within a measurement window, boosting the accuracy up to 90% from <5%. The kinetic signals are organized into a two-dimensional (2D) matrix depending on the sequence context, analogous to an image. A CNN is then applied to the 2D matrix to compute a probabilistic score for the methylation status of a CpG site. Even when trained on just 300,000 data points, the HK model achieves an area under the receiver operating characteristic (ROC) curve (AUC) of 0.95 in differentiating methylated and unmethylated cytosines. The HK model has proved to be a valuable technology in the methylation analysis of long cfDNA (>500 bp), which generally carries more CpG and SNPs than short fragments, and so intrinsically phases these informative loci to augment the power of disease detection (Yu et al. 2021, 2023a). Notably, Choy and colleagues (2022) use the HK model to determine the tissue of origin of individual long cfDNA molecules for the detection of HCC (AUC = 0.91). In addition, various deep learning algorithms have also been applied in nanopore sequencing for basecalling and detection of base modifications in a variety of biological contexts (Boža et al. 2017; Rang et al. 2018; Wick et al. 2019; Grumaz et al. 2020; Neumann et al. 2022; Yu et al. 2023b; Chan et al. 2024).

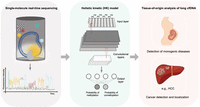
    Figure 2.
    View larger version:
    Figure 2.

    An example of AI-based technology for direct methylation analysis and its clinical applications on the basis of the holistic kinetic (HK) model. (Left) The principle of single-molecule real-time (SMRT) sequencing. Circular DNA templates are incorporated with nucleotides labeled with different fluorophores by a DNA polymerase located in a zero-mode waveguide (ZMW). During DNA polymerization, the kinetics of nucleotide incorporation, including inter-pulse duration (IPD) and pulse width (PW), are affected by base modifications. (Middle) The HK model, an AI-based method that employs a convolutional neural network (CNN). This model is trained using combined kinetic signals and sequence context from a large amount of measurement windows and is applied to the prediction of cytosine methylation status. The methylation probability for the CpG sites, ranging from zero to one, is computed using a sigmoid function at the output layer. (Right) Selected clinical applications of the HK model: (1) deducing the placenta-derived cfDNA by the methylation pattern of long cfDNA molecules, opening up possibilities of developing generic approaches for monogenetic diseases, and (2) detecting patients with cancers and determining the tumor origin of cancer (e.g., hepatocellular carcinoma [HCC]) according to methylation patterns of long cfDNA determined by the HK model.

    The transformer has driven a recent revolution in deep learning (Vaswani et al. 2017; Lin et al. 2022). Transformers use a technique called multihead attention (Vaswani et al. 2017; de Santana Correia and Colombini 2022). First, the sequential data are broken down into “tokens,” which is the smallest unit of data that can be converted into a meaningful numerical representation for the model. Essentially, for each token, its relationships with other tokens are computed by a series of operations, and this is performed massively in parallel to capture different aspects of the relationships between tokens. These massively parallel operations of multihead attention in transformers are more computationally efficient and scalable than recurrent neural networks (RNNs), which perform operations sequentially, with each step depending on the output of the previous step.

    The rise of transformers has led to exciting possibilities on the interface between AI and biology, for which protein structure prediction is a landmark example. In 2020, AlphaFold was able to predict the 3D structure of most proteins from the primary sequence to near-experimental accuracy using a DNN trained on 29,427 peptides (Senior et al. 2019, 2020). Just a year later, AlphaFold2 was launched, using a transformer architecture trained on 107 peptides to obtain accuracy competitive with experimental techniques such as X-ray crystallography (Jumper et al. 2021). AlphaFold3 extends its predictive power to protein–ligand, protein–nucleic acid, and antibody–antigen interactions (Abramson et al. 2024), demonstrating the generalizability of the transformer-based model. The success of AlphaFold has sparked great interest in adopting AI technologies in structural biology and beyond. More recently, ChatGPT has been an unprecedented success of the transformer architecture, using a large language model (LLM) with 175 billion parameters (as of GPT-3) trained on massive web corpora (Brown et al. 2020). The newest version, ChatGPT4, integrates text, vision, and audio into one unified model, marking an important step toward multimodal human–machine interaction. Inspired by ChatGPT, LLMs have also been used to predict protein structure, evolution, and function with high confidence and speed without the need for multiple sequence alignment (Rives et al. 2021; Chowdhury et al. 2022; Lin et al. 2023; Johnson et al. 2024) and also to predict the effects of all approximately 450 million missense variants documented in the human genome (Brandes et al. 2023). In the cfDNA context, the recently invented HK model 2 (X Hu, Y Shi, SH Cheng, et al., in prep.) integrates a transformer architecture with the previously described CNN in HK model 1 (Tse et al. 2021), demonstrating enhanced 5mC versus C detection (AUC = 0.99) and HCC detection (AUC = 0.91) from plasma cfDNA. HK model 2 can also robustly distinguish 5hmC from 5mC (AUC = 0.97) and 6mA from A (AUC = 0.99).

    Too many dimensions spoil the model

    The huge number of tuning parameters in deep learning models necessitates the availability of large-scale training data sets. Adequate training data are crucial to combat the “curse” of dimensionality (Bellman 1961; Altman and Krzywinski 2018): In high-dimensional spaces, data become increasingly sparse as the search space grows exponentially with the dimensionality, and so, it becomes difficult to collect data that are representative of the population or to draw meaningful conclusions. As the flexibility of the prediction equations increases with dimensionality, the model becomes more prone to overfitting, which is when the model parameters capture intrinsic noise in the training data (Ying 2019). If the number of training samples is not proportionate to the number of parameters, even random noise can have undue effects on the model. Overfitted models perform poorly on new data sets and so are unreliable for making diagnostic decisions when faced with multifaceted clinical data. Despite the growing abundance of data available for training, data scarcity is still a major challenge when training deep learning models. On the other hand, classical ML algorithms may perform better in these instances, as their simplicity and reduced complexity allow them to adapt well to a smaller sample size, resulting in more stable and reliable model performance. Regardless of the model, a variety of approaches should be carefully considered in order to protect against overfitting, including dimensionality reduction and regularization, as well as model evaluation methods such as cross-validation and bootstrapping.

    Dimensionality reduction and regularization

    The “curse” of dimensionality may intuitively be addressed by reducing the number of dimensions of the parameter space by remapping the effective information to fewer dimensions through feature engineering algorithms (Jia et al. 2022) such as principal component analysis (PCA) and nonnegative matrix factorization (NMF). Along with reducing the number of dimensions, the effective size of each dimension can be constrained through regularization techniques. Regularization is an operation of deliberately calibrating model parameters to prevent overfitting or underfitting. Explicit regularization techniques in classical ML include L1 and L2 regularizations, which are used in ridge and LASSO regression, respectively, to shrink coefficients toward zero, so that no parameter unduly influences the model (Emmert-Streib and Dehmer 2019). In deep learning, early stopping during training and dropout of a certain proportion of neurons are important regularization algorithms that guard against overfitting (Greener et al. 2022). By concurrently monitoring the model performance on a validation set while training the model, early stopping halts model training when the validation performance begins to degrade. Dropout involves randomly excluding a fraction of the neurons during each training iteration, which theoretically prevents the model from overrelying on any single neuron, and also acts as an internal cross-validation mechanism.

    Model evaluation

    Cross-validation is an important step in ML model evaluation to monitor overfitting by training the model on different subsets of the training data and estimating the expected test error (Arlot and Celisse 2010; Ghojogh and Crowley 2023). Essentially, a data set containing n samples is split into k groups (also known as “folds”), the model is trained on k-1 groups, and then the model is used to predict the response of the remaining group (i.e., the validation/test set). If the model is overfit, the training error will be very small, but the test error will be large. By assessing the degree of model overfitting, cross-validation informs the maximum complexity to which the model can be trained before overfitting is risked.

    For cross-validation, there exists a variety of splitting strategies, reviewed extensively elsewhere (Arlot and Celisse 2010). nCk is often computationally intractable, so partial data splitting methods such as k-fold cross-validation are used (Arlot and Celisse 2010). Crucially, the assumption that the data are independent and identically distributed (i.i.d.) must be examined: If a pair of samples are dependent, possibly because of confounding effects, having one sample in the training set and the other in the validation set would lead to “leakage” (discussed later). To address structural or temporal dependencies, blocked cross-validation may be considered, in which samples are partitioned into “blocks” whose size depends on the strength of correlation (Roberts et al. 2017; Yates et al. 2023).

    In bootstrapping (Efron 1979), the training set is randomly sampled with replacements so that each bootstrap set is the same size as the training set. Applying the model to each bootstrap set gives a distribution of model prediction values. Simulations show that bootstrapping can perform comparably to k-fold cross-validation for model evaluation, the tradeoff being that it is more computationally expensive (Breiman and Spector 1992). In the majority of cases, the bootstrap distribution converges to the true population distribution as the number of bootstrap iterations tends to infinity (Chernick and LaBudde 2014). However, similar to cross-validation, bootstrapping may give inconsistent results if the sample size is too small or if the data are not i.i.d. (Chernick and LaBudde 2014).

    Below, we shall discuss the applications of classical ML and deep learning–based AI technologies in NIPT, cancer liquid biopsies, and the development of the field of cfDNA fragmentomics (Fig. 3).

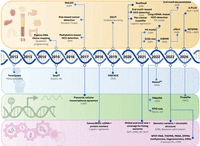
    Figure 3.
    View larger version:
    Figure 3.

    A timeline of applications of AI/ML algorithms to cfDNA analyses. Categories, from top to bottom: (orange) tissue-of-origin analyses and cancer liquid biopsies; (blue) noninvasive prenatal testing, including fetal fraction estimations; (green) fragmentomic-based methylomic and transcriptomic analyses; and (purple) multimodal cfDNA analyses, which leverage different cfDNA features in an integrated model. The name or a brief description of the technology is listed in bold, with the AI/ML algorithms used given below.

    Previous SectionNext Section

    Noninvasive prenatal testing

    The discovery of cell-free fetal DNA in maternal plasma (Lo et al. 1997) has facilitated a paradigm shift in prenatal testing, enabling applications such as noninvasive fetal RhD blood group genotyping (Lo et al. 1998a; Finning et al. 2008; Legler et al. 2021; Alford et al. 2023) fetal sex determination (Costa et al. 2002; Raman et al. 2019; Wu et al. 2023), detection of fetal chromosomal aneuploidies (Lo et al. 2007; Chiu et al. 2008, 2009, 2011; Fan et al. 2008; Straver et al. 2014; Yang et al. 2018; Paluoja et al. 2021; Lee et al. 2022a; Dar et al. 2022b; Schlaikjær Hartwig et al. 2023), subchromosomal structural aberrations (Fan et al. 2012; Srinivasan et al. 2013; Yu et al. 2013; Dar et al. 2022a), and diagnosis of monogenic diseases (Lo et al. 2010; Tsui et al. 2011; Lam et al. 2012; Ma et al. 2014; New et al. 2014; Yoo et al. 2015; Mohan et al. 2022).

    NIPT requires sufficient fetal DNA amounts in a maternal sample, quantified as the fetal DNA fraction, for analytical and statistical robustness. The fetal DNA fraction is incorporated in mathematical models for calling fetal aneuploidies, such as in Illumina's VeriSeq NIPT solution v2 assay, and also for single gene disorder analysis. For the latter, relative mutation dosage (RMD) (Lun et al. 2008) and relative haplotype dosage (RHDO) (Lo et al. 2010) establish statistical thresholds for classifying fetal monogenic disorders from maternal plasma DNA analysis. RMD quantifies the allelic imbalance at a maternally heterozygous SNP (AB), in which the fetus being homozygous at that locus (AA/BB) would imbalance the allelic counts (Lun et al. 2008). In contrast to RMD, which analyzes a single genomic locus, RHDO uses parental genotypes to phase a series of fetal SNPs into haplotypes, increasing the performance of the analysis. A fetal DNA fraction of <4% would be commonly considered as “QC failure” for fetal chromosomal aneuploidy detection (Norton et al. 2012), although lower limits of down to 2% have been suggested (Fiorentino et al. 2016), and the threshold may vary according to the analytical platform used (Hestand et al. 2019; Becking et al. 2023).

    Many methodologies have been developed to estimate the fetal DNA fraction in maternal plasma samples. Some approaches leverage fetal-specific sequences that are absent from the mother's genome, such as Y Chromosome–specific sequences (Lo et al. 1998b) and other paternally inherited sequences (Lo et al. 2010). Fetal-specific paternally inherited alleles include single-nucleotide polymorphisms (SNPs) in which the father is homozygous for a variant (AA) not carried by the mother (BB), and the fetal DNA fraction can be estimated by the ratio of A to B alleles in maternal plasma. However, Y-Chromosome analysis is only applicable to male fetuses. Methods that need parental genotypic information may present practical challenges, because only maternal blood samples would be collected for NIPT in most clinical settings, and the paternal genotype information may not be accurate owing to nonpaternity (Deignan et al. 2020).

    To circumvent these difficulties, Jiang and colleagues (2012) developed a binomial mixture model (FetalQuant) that utilized maximum likelihood to estimate the fetal DNA fraction directly from target capture sequencing of maternal plasma. The allele ratios observed in maternal plasma would depend on the maternal and fetal genotypes and the fetal DNA fraction. At each SNP, there are four possible combinations of maternal and fetal genotypes: AAAA, AAAB, ABAA, and ABAB, in which the main text and subscript represent the maternal and fetal genotypes, respectively. If the fetal DNA fraction is f, the expected B allele fraction for each maternal–fetal genotype combination would be zero, f/2, 0.5 − f/2, and 0.5, respectively. As the allelic counts at each SNP follow a binomial distribution depending on the genotype combination, a binomial mixture model can be constructed using four binomial distributions parameterized by the expected B allele fractions. The fetal DNA fraction was iteratively tuned using expectation-maximization by fitting the observed allele ratios. An extension of this is that significant deviation from the expected allelic fractions for some SNPs may indicate fetal aneuploidy of a specific chromosome. Sparks and colleagues (2012) applied this algorithm to model allelic ratios in maternal plasma for fetal chromosomal aneuploidy detection, named FORTE.

    Motivated by the differential cfDNA fragmentation patterns existing between fetal and maternal genomes (Lo et al. 2010), a generic method called SeqFF was developed to deduce the fetal DNA fraction from the same sequencing data used to generate the routine NIPT result, without any additional assays (Kim et al. 2015). SeqFF is based on the sequencing coverage signals across nonoverlapping 50 kb bins genome-wide (Fig. 1). The normalized read counts across bins were fitted into both a high-dimensional elastic net and a reduced-rank regression model with respect to fetal DNA fractions. Simple linear regression is the most straightforward approach to make predictions when a linear relationship between the features and outcomes is assumed, and it is fit by minimizing the cost function (sum of squared residuals), which parameterizes the difference between the predicted and observed values. However, it does not include any automated mechanism for feature selection: Each feature included in the model contributes to the explanation of the variance in the outcomes, regardless of the significance of its contribution, and is thus prone to overfitting when a large number of features is used (Bartlett et al. 2020). To protect against overfitting, regularization techniques penalize both the number and magnitude of the regression coefficients, such that the most informative coefficients are selected to meaningfully affect the model (Emmert-Streib and Dehmer 2019). Ridge regression (Hoerl and Kennard 1970) includes a regularization term that is added to the regression cost function, which forces less informative coefficients toward (but not exactly) zero. Although ridge regression can handle multicollinearity better than simple linear regression, it introduces bias to the model. Another regularization method is LASSO (Tibshirani 1996; Li et al. 2022), which is similar to ridge regression, but it assumes that the coefficients of the linear model are sparse, and hence, it shrinks the less informative coefficients to exactly zero. However, in some scenarios, an overstrict LASSO might overkill potentially informative features. Elastic net (Zou and Hastie 2005; Tay et al. 2023) combines both ridge and LASSO regression to attenuate their respective shortcomings, improving model accuracy and robustness. Importantly, elastic net introduces a key tuning parameter that balances the L1 and L2 regularization terms and thus achieves a compromise between variable selection and parameter shrinkage. Training of the elastic net used plasma sequencing data from 25,312 pregnant women and achieved a Pearson's correlation of >0.9 between predicted and actual fetal DNA fraction when applied to a validation set of 505 pregnant women (Kim et al. 2015). The results from the elastic net were averaged with those from reduced-rank regression to give the final fetal fraction estimate. In conclusion, SeqFF is applicable to both male and female pregnancies, can be integrated without additional cost into routine NIPT, and can greatly improve the accuracy of NIPT for fetal copy number aberrations.

    More recently, deep learning has been applied to fetal fraction estimation in the PREFACE pipeline (Raman et al. 2019). Similar to SeqFF, PREFACE also uses local coverage information in genomic bins as its input variables, which are clustered into a set of linearly uncorrelated components by PCA. These new parameters are then fed into a DNN with two hidden layers to estimate fetal fraction, trained on the values obtained from Y-Chromosome count analysis. The parameter weights in the DNN are cross-validated with ordinary least-square regression to ensure robustness. PREFACE generally performs better than the traditional elastic net, achieving a Pearson's correlation of up to 0.940 (Raman et al. 2019).

    The set of informative features used to establish a model is as important as the selection of an appropriate model, in order to avoid overfitting and circularity. Notably, SeqFF and PREFACE exclude windows located on Chromosomes 13, 18, and 21 from the model, as the copy number variation can also be used to estimate fetal DNA fraction (Yu et al. 2017). Because the training data set might include fetal aneuploidies, the model may wrongly predict that loci on Chromosomes 13, 18, and 21 are highly associated with fetal fraction (Raman et al. 2019). As SeqFF does not rely on sex chromosome reads like PREFACE, SeqFF also excludes windows on Chromosomes X and Y because of possible sex chromosome aneuploidies (Kim et al. 2015).

    Although NIPT for fetal chromosomal aneuploidies boasts high sensitivity and specificity (Chiu et al. 2008, 2011), its performance in detecting fetal subchromosomal aberrations significantly diminishes. This reduction in robustness is owing to the decreased number of sequenced fragments in the affected genomic regions, which increases sampling variation and reduces the sensitivity of the z-score approach. ML is emerging as a potential method to attenuate this decreased statistical robustness by holistically analyzing aberrant signals. Notably, Dar and colleagues (2022a) constructed an ensemble of DNNs to learn the linkages between SNPs from 1.6 million maternal plasma sequencing samples, which was used for the prenatal screening of the 22q11.2 microdeletion at much lower coverage than classical read count-based approaches (Fig. 1). Beyond the more popular applications of NIPT to chromosomal aneuploidies, structural aberrations, and fetal monogenic diseases, ML could offer alternative pathways to the screening for other maternal complications, such as diagnosis of preeclampsia or prediction of miscarriage.

    Previous SectionNext Section

    Genetic mutation–based cancer liquid biopsies

    Early attempts to leverage ctDNA as a cancer biomarker were based on the detection of tumor-specific genetic mutations, reviewed elsewhere (Wan et al. 2017). Although genetic aberrations such as point mutations commonly occur in cancer genomes, the proportion of fragments that may harbor tumor-specific mutations is often low, typically in patients with early-stage tumors. Thus, it is challenging to differentiate true variants from overwhelming background noises that could have been introduced in library preparation and sequencing. Historically, studies sought to overcome this difficulty by using targeted deep sequencing of multiple loci in parallel (Forshew et al. 2012; Murtaza et al. 2013), but their efficacy may be limited by low variant allele frequency in the blood circulation, and also the wide heterogeneity of cancer genomes among different patients.

    More recent attempts at cancer SNV detection (Newman et al. 2016; Chabon et al. 2020; Li et al. 2021b, 2023a; Christensen et al. 2023; Widman et al. 2024) implement ML algorithms to distinguish true cancer-associated variants from preanalytical or analytical errors. In particular, cfSNV (Li et al. 2021b, 2023a) and MRD-EDGESNV (Widman et al. 2024) demonstrate robust tumor mutation detection without the need for deep tumor tissue sequencing. However, cfSNV requires matched white blood cell sequencing data to remove nontumor clonal hematopoietic mutations from the analysis. MRD-EDGESNV uses a CNN to analyze SNVs in their sequence context and uses a multilayer perceptron framework to integrate other fragmentomic features such as size and chromatin accessibility. When applied to the detection of melanoma, a cancer well known to involve specific mutational signatures (Brash 2015; Alexandrov et al. 2020), MRD-EDGESNV achieves an AUC of 0.94.

    In contrast to somatic mutations, methylomic and fragmentomic alterations can span millions of genomic coordinates, and thus, these perturbations may be more readily detected even at shallow-depth sequencing. Methylomics and fragmentomics also encode tissue-specific information, enabling diseases to be localized to their tissue of origin. Below, we discuss some exemplary studies that use classical ML- or AI-based technologies to perform cancer liquid biopsies, as well as highlight the importance of appropriate marker selection.

    Previous SectionNext Section

    Methylation-based cancer liquid biopsies

    The tissue of origin of cfDNA is encoded in their biological properties, offering many opportunities for developing tissue-specific diagnostic tools for cancer. These properties include methylation patterns (Lun et al. 2013; Sun et al. 2015; Moss et al. 2018), fragmentomics (Chan et al. 2004; Lo et al. 2010; Yu et al. 2014; Jiang et al. 2015, 2018, 2020b; Chan et al. 2016), and histone modifications (Gezer et al. 2015; Sadeh et al. 2021; Fedyuk et al. 2023). With the abundance of available sequencing data, many attempts have used classical ML algorithms such as SVMs and decision trees to leverage these properties for cancer detection. In the 2020s, deep learning is becoming increasingly exploited in this area, supported by large-scale clinical studies.

    Decoding tissue-of-origin information in cfDNA methylation patterns

    Sun and colleagues (2015) demonstrated that the methylation profile of plasma DNA could be deconvoluted into methylation profiles of various tissues linearly weighted by their contributions, thus allowing for the deduction of proportional contributions of various tissues into the plasma DNA pool, referred to as plasma DNA tissue mapping. This approach made use of 5820 tissue-associated methylation markers from 14 tissues including the liver, lungs, esophagus, heart, pancreas, colon, small intestines, adipose tissues, adrenal glands, brain, T cells, B cells, and neutrophils. These markers were selected because they were either (1) specific to one particular tissue (type I) or (2) highly variable among all tissues analyzed (type II). For the final model, 1013 type I markers and 4807 type II markers were selected (Sun et al. 2015). The methylation level of such a marker in the plasma is theoretically equal to the sum of tissue-specific methylation weighted by the tissue percentage contributions. Thus, a system of simultaneous equations can be constructed, one for each marker, and quadratic programming (Van den Meersche et al. 2009) was used to obtain the proportional contributions from different tissues. Quadratic programming is an unsupervised learning algorithm that iteratively finds the vertex of a quadratic objective function without the requirement of prior training. In plasma DNA tissue mapping, the proportional contributions from different tissues are estimated in a way that minimizes the quadratic cost function. The validity of the plasma DNA tissue mapping was supported by the agreement between the placental contribution and fetal DNA fraction (Pearson's r = 0.99) in pregnant women, as well as the high correlation between the liver contribution and donor liver DNA fraction in plasma of patients with liver transplantation (Pearson's r = 0.99), using gold-standard SNP-based approaches as previously described (Lo et al. 2010; Zheng et al. 2012). Plasma DNA tissue mapping also revealed that the organs suffering from cancer generally shed more DNA into plasma: For example, patients with HCC had higher liver contribution than those without. More importantly, by analyzing cfDNA molecules originating from regions with copy number variants, the anatomical site affected by the malignancy could be pinpointed. This principle for plasma DNA tissue mapping has been further extended by many other studies (Kang et al. 2017; Moss et al. 2018; Sun et al. 2022). As tissues usually have some heterogeneity in cell type, cell-type resolution of methylation patterns (Loyfer et al. 2023) would further enhance the resolution and accuracy of plasma DNA tissue deconvolution. For example, Loyfer and colleagues (2023) demonstrated the ability to differentiate the contributions of megakaryocytes and erythrocytes (i.e., 31% and 5%, respectively), even though they are derived from common progenitors.

    Plasma DNA tissue mapping identifies that neutrophils, lymphocytes, and the liver (and, in pregnant women, the placenta) are the main contributors to plasma cfDNA. Using high-resolution methylation atlases, cfDNA of megakaryocyte origin has also been identified (Moss et al. 2023). However, to further extend the resolution for plasma DNA tissue mapping, a number of algorithms have recently been developed that are based on deep learning. Li and colleagues (2023b) developed cfSort for tissue deconvolution of cfDNA. Similar to the plasma DNA tissue mapping described previously (Sun et al. 2015), methylation markers were selected for training the deep learning model. In addition to the type I markers as defined previously (markers specific to one tissue), the authors also selected markers that show differential methylation between two tissue groups defined by developmental phylogeny, for example, the digestive system and lymphatic system (here defined as type II), and markers that show differential methylation between two tissue types, which could help distinguish similar tissue types from adjacent organs, such as the esophagus and stomach (type III). A total of 51,035 markers were identified (3775 type I markers, 6660 type II markers, and 40,600 type III markers), which were grouped using k-means clustering to merge individual tissue markers into 10,183 marker clusters. For every marker cluster, the fraction of tissue-specific DNA fragments at all markers within the cluster was calculated, which was used as the input vector for two DNNs with three dense hidden layers each. To avoid model overfitting, a batch normalization layer was used before each dense layer, followed by a dropout layer that prunes relatively unimportant nodes from the model. The predicted fractional tissue contributions were determined by averaging the predictions from the two DNNs. cfSort was reported to potentially outperform existing methods in terms of accuracy and detection limit.

    cfDNA methylation–based cancer detection, localization, and staging

    DNA methylation at the cellular level is cell type specific (Loyfer et al. 2023) and tumor specific (Liang et al. 2023). Thus, it is theoretically possible to infer the tissue of origin of ctDNA and the type of cancer. Indeed, Sun and colleagues (2015) had demonstrated the feasibility of tracing the tumor origin on the basis of plasma DNA methylation patterns. Briefly, this method leverages genomic regions that exhibit copy number variants in cancer. The prevalence of tissue-specific methylation markers in these genomic regions would theoretically show the largest deviation from normal (ΔMtissue) in cfDNA released from the tumor tissue of origin. ΔMtissue was able to pinpoint the tumor tissue of origin in both HCC and lymphoma patients. Subsequently, a number of studies have leveraged classical ML (Guo et al. 2017; Xu et al. 2017; Li et al. 2018; Shen et al. 2018; Liu et al. 2020; Liang et al. 2021; Stackpole et al. 2022; Gao et al. 2023) and deep learning (Peneder et al. 2021; Li et al. 2021a; Abbosh et al. 2023) for cancer detection, localization, staging, and prognosis based on cfDNA methylation information.

    Marker selection prior to the main learning task was approached diligently. For example, Xu and colleagues (2017) implemented a pipeline that narrowed down 485,000 CpGs from The Cancer Genome Atlas (TCGA) and Gene Expression Omnibus (GEO) to only 10 markers in the two final learning tasks for HCC detection. First, the 1000 CpGs that showed the most significantly different methylation rates between HCC and healthy control plasma were selected using a moderated t-test. Out of these 1000, 401 markers were validated using targeted BS-seq in 28 paired HCC tissue DNA and plasma cfDNA samples. These 401 markers were further filtered using random forest (RF) (Breiman 2001) and LASSO independently. RF constructs decision trees on bootstraps of the training data and averages the results from all trees. Combining multiple decisions often increases the robustness of the model (Dietterich 2000). Many authors propose that RF is inherently resistant to overfitting from a mathematical perspective, as increasing the number of trees decreases the model variance but does not lead to overfitting (Hastie et al. 2009; Biau and Scornet 2016; Barreñada et al. 2024). However, RF can overfit if the trees are grown too deeply (Barreñada et al. 2024). RF and LASSO identified 24 and 30 markers, respectively, in which 10 markers were identified by both algorithms. Finally, these 10 markers served as the input variables for the main classification task, which was performed robustly by logistic regression (AUC = 0.944 on validation) and unsupervised hierarchical clustering.

    Liang and colleagues (2021) developed a deep methylation sequencing approach (ELSA-seq) that identifies methylation patterns at high resolution and implemented a ML classifier to distinguish lung cancer patients from sex-matched healthy controls. The authors took a different approach to that of Xu and colleagues regarding marker selection, in that they defined methylation “blocks” in which the methylation status of the CpGs was similar and closely linked. From 80,672 raw CpGs taken from TCGA and GEO, the authors defined 8312 methylation blocks. The authors argued that in silico binning of CpGs protects against sampling variance and technical noise, which would be more significant on individual CpGs. Then, a subset of 2473 blocks that were most informative for lung cancer were selected for the final classification task, which was done using a soft-margin SVM (Fig. 1). An SVM is a classical supervised learning algorithm that classifies data points by learning the boundary that separates the classes. This boundary is called the maximum-margin hyperplane, as it maximizes the distance between itself and the nearest point from two classes. In high-dimensional space, classes are often not linearly separable, so sometimes a “soft margin” is implemented to allow for a few anomalous misclassified points with a certain penalty, reducing the risk of overfitting on noisy data. The SVM achieves an AUC of 0.93 and 0.90 on the training/validation and single-blind test sets, respectively.

    The first commercially available pan-cancer detection assay was developed by Liu and colleagues (2020), who systematically assessed the performance of methylation pattern–based detection and localization of 12 cancer types across all four stages, using data from the Circulating Cell-free Genome Atlas (CCGA). A total of 15,254 plasma DNA samples with (n = 8584; 56%) and without (n = 6670; 44%) cancer was collected from 142 sites in North America in the CCGA. The authors first identified genomic regions that were most likely to contain cancer- or tissue-specific methylation patterns. Then, after bisulfite treatment of the plasma DNA samples, cfDNA fragments in these regions were enriched using biotinylated probes, and a panel of 1,116,720 CpGs was then selected from the probes. After assembly in silico into <1 kb contiguous regions, a Bernoulli mixture model was trained using maximum likelihood to compute the probability that the fragments originated from specific source populations (i.e., individuals with cancer originating from a particular tissue). Each region was then ranked by its ability to differentiate between cancer types or from noncancer, and the top 256 regions for each cancer type were selected for the final analysis. On this final panel, a binomial logistic regression model was trained to differentiate cancer and noncancer signals, whereas a multinomial logistic regression model was trained to classify the tissue source of cancer. This ensemble achieved an overall specificity of 99.3%, a sensitivity of 67.3% for stage I–III cancers, and an accuracy of 93% in the tissue-of-origin analysis, outperforming classical pan-cancer detection approaches such as WGS and targeted mutation panels.

    Several studies (Peneder et al. 2021; Li et al. 2021a; Jamshidi et al. 2022) highlight the potential of deep learning in noninvasive cancer detection across a variety of modalities, particularly because of their high flexibility of model structure, and the value of deep learning in cfDNA methylation-based cancer detection has been increasingly recognized. An example of this is DISMIR, a deep learning–based HCC classifier that integrates methylation and surrounding sequence information using convolutional and recurrent architectures (Li et al. 2021a). First, the most informative HCC-specific differentially methylated regions referred to as “switching regions” were identified, which showed above-threshold hypomethylation compared with the background methylation rate around that locus. Each “switching region” was encoded as a matrix upon which a convolutional layer was applied. Then, a recurrent layer (bidirectional long short-term memory) captures the sequential information in both forward and backward directions, followed by another 1D convolution. Finally, a DNN was applied to ultimately generate a continuous score that parameterizes the probability that the read is from a cancer tissue. DISMIR achieves an AUC of 0.99 for distinguishing HCC from healthy controls and is much more resistant to low sequencing depth (AUC = 0.91 at 0.01–0.1×) than a previous classical ML-based method by the same authors (AUC = 0.74) (Li et al. 2018). However, multicenter large-scale clinical trials across different cancer types are still necessary to address the actual benefit of using deep learning algorithms with a large number of parameters, compared with the conventional ML methods with less parameters.

    Previous SectionNext Section

    Fragmentomics

    An emerging paradigm in cfDNA-based diagnostics is the usage of cfDNA fragmentomics, which contain a wealth of information about physiological and pathological conditions. There are many levels to fragmentomics, including cfDNA fragment size (Chan et al. 2004; Lo et al. 2010; Jiang et al. 2015; Underhill et al. 2016; Mouliere et al. 2018; Kwon et al. 2023; Yu et al. 2023b), nucleosome footprints (Snyder et al. 2016; Sun et al. 2019; Yang et al. 2021; Jacob et al. 2024), fragment end motifs (Jiang et al. 2020a; Zhou et al. 2022, 2023), preferred ends (Jiang et al. 2018), and jagged ends (Jiang et al. 2020b; Ding et al. 2022). The richness of the fragmentomic landscape has spurred the development of ML algorithms to leverage fragmentomics in cancer liquid biopsies. Below, we discuss some recent advances in fragmentomics that rely on ML.

    Size profiles

    Perturbations in the cfDNA size profile serve as biomarkers for the detection and monitoring of cancer. However, the overall size profile alone cannot easily distinguish cancer from healthy controls (van der Vaart et al. 2009), and so, enrichment and isolation of the tumor-derived signal are needed. By focusing on chromosome arms that exhibited copy number aberrations in HCC, Jiang and colleagues (2015) discovered that plasma DNA of patients with HCC had aberrant size profiles depending on the tumor-derived DNA fraction and demonstrated that the tumoral cfDNA is shorter than the background cfDNA, which is mainly of hematopoietic origin. Based on this, Moulière and colleagues (2018) found that enriching fragments between 90 and 150 bp improved ctDNA detection and that the proportions of certain size ranges could be used to detect cancer using RF. As a corollary, the size profile across the genome would be dependent on the copy number aberrations present in the tumor cells and on tissue-specific differences in genomic chromatin architecture. This is a supporting biological basis of the DELFI approach (Cristiano et al. 2019), which considers local size profile information in 5 Mb windows across the entire genome. In each window, the ratio of short (100–150 bp) to long (151–200 bp) cfDNA fragments and overall sequencing coverage were used to construct the features to train a gradient boosting algorithm (Fig. 1). Gradient boosting sequentially builds a multitude of weak learners, in which each one is trained to minimize the loss function of the previous model using gradient descent. DELFI had sensitivities of detection ranging from 57% to >99% among seven cancer types at 98% specificity, with an overall AUC of 0.94. Combining DELFI with mutation detection in cfDNA raised the sensitivity to 91% while still at 98% specificity. At a threshold of 95% specificity, 79% of patients with stage I–III cancers could be detected. Moreover, the tissue of origin of the tumor could be identified in 61% of cases. Recently, DELFI has also been applied to diagnose, classify, and predict the prognosis of lung (Mathios et al. 2021) and liver (Foda et al. 2023) cancers.

    End motifs

    Mechanistically, an aspect of the biology that underpins fragmentomics is likely to be the action of nucleases (Han and Lo 2021). Mammalian DNA nucleases are unlike bacterial restriction enzymes (REs): Although RE cutting sites are strictly defined, it is believed that these nucleases exhibit a certain level of preference in the cutting signatures, which can manifest as preferentially generated base sequences at the 5′ ends of cfDNA fragments. However, with increasing resolution, that is, the inclusion of more bases in the end motif, the search space increases exponentially (for a k-mer, there would be 4k end motifs). Earlier work focused on isolating the motifs whose abundances experienced the most significant changes when nuclease activity was perturbed artificially (Serpas et al. 2019; Han et al. 2020) or in pathology (Jiang et al. 2020a). However, only choosing a few specific motifs out of the 256 possible 4-mers would not completely reflect the variety of end motifs that nucleases can generate. Jiang and colleagues (2020a) trained an SVM for distinguishing patients with and without HCC, taking into account all 256 4-mer end motifs, with an AUC of 0.89. This is an improvement on a classifier using the motif diversity score, which parameterizes the diversity of end motifs found in cfDNA fragments. As perturbations in the end motif profile may reflect pathological changes in nuclease action, this is potentially generalizable to a wide range of cancers. For example, one of the major players governing cfDNA fragmentation is DNASE1L3, which is downregulated in many cancers such as colorectal cancer, lung cancer, nasopharyngeal carcinoma, and head and neck squamous cell carcinoma (Jiang et al. 2020a), providing a biological basis for end motif–based pan-cancer detection.

    Zhou and colleagues (2023) used NMF to deconvolute the high-dimensional end motif profile, mathematically deriving six distinct types of cfDNA cleavage patterns, referred to as “founder” end motif profiles (F-profiles) (Fig. 1). NMF is an unsupervised clustering algorithm that approximates a data matrix as the product of (usually) two source matrices (Lee and Seung 1999). Training the algorithm with murine cfDNA samples from different nuclease-knockout mice yielded three F-profiles that were linked to DNASE1L3, DNASE1, and DFFB, and three F-profiles that have not been assigned yet. Interestingly, F-profile VI shows no obvious sequence preference among the 256 4-mer motifs but is able to robustly differentiate HCC patients and HBV carriers (AUC = 0.97), and thus, the authors speculated that it may be related to oxidative stress. The percentage contribution of F-profile I, corresponding to DNASE1L3 action, could inform pathological states such as familial SLE (AUC = 0.97) and HCC (AUC = 0.89), as familial SLE is linked to genetic DNASE1L3 deficiency and HCC with DNASE1L3 downregulation. In summary, NMF can be used for generating testable hypotheses that could yield further insight into the mechanisms of cfDNA fragmentation. However, more work needs to be done to reveal and characterize the biological mechanisms behind the remaining putative components. In particular, the training data used by Zhou and colleagues (2023) only included knockouts of DNASE1L3, DNASE1, and DFFB, but there may be other DNA nucleases at play that need to be investigated further. It remains to be seen whether incorporating more nuclease knockout models into the analysis will reveal novel components of the end motif profile. Interestingly, NMF was also used in a proof-of-concept study to infer the ctDNA size profile and derive cancer-specific and chromatin state–specific size signatures, achieving early detection of various cancers (Renaud et al. 2022).

    Hidden fragmentomic signals in repeat elements

    Based on the knowledge that tumor-derived cfDNA exhibits changes in methylation and fragmentation patterns (Lo et al. 2021), Douville and colleagues (2024) hypothesized that the representation of specific Alu elements might be different in plasma DNA of patients with cancer compared with healthy controls. The abundance of Alu in the human genome lends itself well to ML-based analyses, for which the authors developed a method called Alu profile learning using sequencing (A-PLUS) (Douville et al. 2024). A-PLUS employed a single primer pair to amplify approximately 350,000 Alu elements across the genome. After discarding the elements that were unstable or had insufficient coverage, dimensionality reduction was performed on the remainder using PCA, and the top 60 principal components were selected for the final panel. An SVM was then trained on the 60-marker panel using 7615 samples from 5178 individuals, among which 2073 were solid cancers, obtaining a sensitivity of 40.5% across 11 different cancer types at a specificity of 98.5%. Although it is well known that cancer genomes often exhibit copy number aberrations (Shlien and Malkin 2009; Yi and Ju 2018), A-PLUS could detect 41% of the cancer samples that were not detected by either copy number aberrations or common protein biomarkers (e.g., CA135, AFP, CA15-3); combining A-PLUS with copy number aberrations and eight common protein biomarkers detected 51% of the cancers at a specificity of 98.9%. The authors found that the power of A-PLUS could be partly attributed to the global reduction of AluS subfamily elements in plasma DNA with solid cancers. In a similar vein, another group also demonstrated the application of ML to the analysis of de novo k-mers within 1280 repeat elements for predicting disease in patients with early-stage lung or liver cancer (Annapragada et al. 2024). These recent findings suggest that repeat elements contain novel fragmentomic signals in addition to copy number aberrations and so have the potential to improve existing copy number–based and fragmentomic-based models with their integration.

    Fragmentomic-based inference of methylomic and transcriptomic signals

    With an improved understanding of the biological systems implicated in the cfDNA landscape, it would be greatly informative to consider the links between cfDNA fragmentomics and the underlying methylome and transcriptome. As methylation and gene expression patterns can be tissue and tumor specific, a single fragmentomic assay could have the potential to offer disease detection and tissue-of-origin analysis based on cfDNA sequencing, without having to resort to complicated or low-yield experimental protocols such as BS-seq or RNA sequencing. Indeed, cfDNA fragmentation has been revealed to be closely linked to DNA methylation (Zhou et al. 2022) and gene expression (Ulz et al. 2016; Esfahani et al. 2022), opening possibilities for new diagnostic approaches.

    Zhou and colleagues (2022) developed fragmentomic-based methylation analysis (FRAGMA) based on the realization that fragmentation around a CpG site depends on its methylation status, with twofold higher cleavage at methylated cytosine (5mC) than its unmethylated counterpart. In other words, CpG methylation would elevate the “CGN/NCG ratio” observed at that CpG. This would allow the determination of the methylome from cfDNA sequencing data alone without the need for bisulfite treatment (which is destructive) or currently expensive single-molecule sequencing. In one implementation of FRAGMA, a CNN was implemented to integrate fragmentation information across five consecutive nucleotides on either side of the CpG cytosine for classification of CpG methylation status (Fig. 1). The CNN was trained on cfDNA cleavage patterns associated with a number of hypermethylated and hypomethylated CpG sites, achieving an AUC of 0.93 for differentiation between methylated and unmethylated cytosines. The authors also successfully used CGN/NCG ratios across all eight CG-containing motifs to train an SVM to distinguish HCC from non-HCC individuals at a specificity of 96% (AUC = 0.98).

    Based on this knowledge, there has also been a recent effort to predict CpG methylation from shallow-depth cfDNA WGS using a hidden Markov model (HMM), which the authors called FinaleMe (Liu et al. 2024b). HMMs model a chain of observable probabilistic processes that depend on “hidden” internal factors: In this case, the observations are the fragment lengths, normalized coverage, and the position of the CpG in the fragment. FinaleMe assumed that the CpG methylation status was a multivariate Gaussian distribution of these three fragmentomic features. Then, the key training step in an HMM was to determine the transition and emission probabilities. In FinaleMe, the emission probabilities for the three fragmentomic features were learned (i.e., the likelihood of making such an observation given an underlying methylation state), whereas the transition probabilities were precalculated based on the distance between each pair of adjacent CpG sites. Finally, the authors used the Viterbi algorithm (Viterbi 1967; Forney 1973) to estimate the methylation status of each CpG with an AUC of 0.91 for CpGs at fragments with five or more CpGs.

    In addition to the deduction of DNA methylation signals, transcriptomic analysis from cfDNA fragmentomics is being actively pursued. Theoretically, transcriptionally active promoters would be less protected by nucleosomes, which would result in a more random cleavage pattern than that of inactive promoters. Based on this hypothesis, Esfahani and colleagues (2022) developed an approach, named epigenetic expression inference from cell-free DNA sequencing (EPIC-seq), that inferred RNA expression from the cfDNA fragmentation profile around the transcriptional start site (TSS). To estimate the RNA expression, the authors performed deep sequencing of TSS-flanking regions in cfDNA to obtain the diversity of fragment sizes, parameterized as promoter fragmentation entropy (PFE), which was then used to estimate gene expression using an ensemble of linear models. These estimated expression levels were used to train an elastic net logistic regression model for non-small-cell lung cancer (NSCLC) detection (AUC = 0.91) and subtype classification (AUC = 0.90). As expected, the genes with the largest coefficients included canonical markers for lung adenocarcinoma and squamous cell carcinoma, highlighting the importance of biological validation of conclusions drawn from ML.

    Although these recent approaches hold significant promise, their true sensitivity, specificity, and clinical value are required to be further confirmed through extensive multicenter trials. Data gathered from these large-scale trials would open up exciting possibilities for exploring more complex AI-based models for healthcare. These more sophisticated models, like transformer-based LLMs, often require huge sample sizes to achieve their full potential. The interplay between methylation- and transcription-associated cfDNA fragmentation features, sample sizes, and model complexity may shape the future dynamic landscape of AI-based noninvasive diagnostics. It is worth noting that although the review has presented various methodologies, there remains a significant gap in direct comparative analysis between these approaches. Such comparisons are essential to accurately assess the true efficacy and potential collaborative benefits of these technologies.

    Previous SectionNext Section

    Common pitfalls

    The amount of cfDNA sequencing data, coupled with the accessibility of ML toolkits, has driven the increasingly popular application of various ML algorithms to cfDNA analyses. However, an awareness of the possible pitfalls in pipeline design is paramount in ensuring that the model will be robust on unseen data or yield any reliable mechanistic insight. Common pitfalls general to ML in genomics have been reviewed elsewhere (Whalen et al. 2022). Here we discuss two pitfalls that may be particularly pertinent in the field of cfDNA-based diagnostics and highlight examples of previous research that addresses them.

    Confounding effects

    Confounders are unmeasured variables that induce dependence between predictor variables and output. If confounding effects are not accounted for, the biological interpretations of the learned predictor–output relationships may be invalid, and the model may perform poorly when the confounder is eliminated or distributed differently. A classic example of a confounder is ancestry in genetic association studies (Kittles and Weiss 2003; Tang et al. 2005; Sohail et al. 2019). Confounding effects introduce bias in the training data, and it is well known that ML classifiers can be prone to amplifying these inherent biases (Zhao et al. 2017; Hall et al. 2022).

    In the context of cfDNA-based diagnostics, batch effects resulting from preanalytical or analytical factors may be a pervasive source of confounders. It has been shown that plasma cfDNA end motifs obtained from different processing centers using the same preparation protocol may cluster separately (van der Pol et al. 2022). Physiological variables such as gender and BMI may also be associated with differences in cfDNA parameters. In particular, increased maternal BMI was shown to be associated with low fetal fraction in multiple large-scale clinical studies (Wang et al. 2013; Hou et al. 2019; Pan et al. 2024). Furthermore, environmental factors influencing physiological behavior may also have measurable effects. For example, it was previously identified that lower ambient temperatures of blood collection were independently associated with increased plasma EBV DNA, which the authors attributed to impairment of the immune response allowing transient viral replication in cold temperatures (Chan et al. 2018).

    Methods of addressing batch effects, including study design considerations and quality-control analyses such as hierarchical clustering, are reviewed elsewhere (Leek et al. 2010). For example, Liang and colleagues (2021) explicitly address and minimize possible batch effects by recruiting independently from two hospitals and processing cancer and control samples together. It may also be important in the future to establish external validation controls for emerging areas of cfDNA biology such as fragmentomics (van der Pol et al. 2022).

    Leakage

    It may be ideal that a model is built only on the training data set, namely, without any dependence on the validation data set, to ensure that the testing phase is fair. Information “leakage” from the validation into the training set because of an unsound data preprocessing pipeline may cause spurious circular relationships between the independent and dependent variables (Pulini et al. 2019; Whalen et al. 2022; Kapoor and Narayanan 2023). Indeed, many authors have identified leakage as a major cause of overoptimism in ML-based predictions across many fields of science (Rocke et al. 2009; Pulini et al. 2019; Kapoor and Narayanan 2023). When leakage is corrected for in these instances, the ML model may not even exhibit meaningful improvement over classical statistical models (Kapoor and Narayanan 2023). Dependency between samples may also contribute to leakage (Whalen et al. 2022), for which blocked cross-validation should be considered (Roberts et al. 2017; Yates et al. 2023).

    Leakage is particularly relevant in cases in which feature selection must be performed: For example, selection of a panel of differentially methylated regions, from which an ML classifier is built. In particular, Whalen and colleagues (2022) warn against selecting such a methylation panel from the whole data set before cross-validation. Given that much work in cfDNA-based diagnostics involves extracting and selecting methylomic information for the final classification step, this consideration of leakage is particularly important. Liu and colleagues (2020) demonstrate commendable diligence in pipeline design: In particular, it was clear that the validation data set was not released until the final classifiers were trained and locked, and all analyses were double-blinded.

    Previous SectionNext Section

    Future directions and concluding remarks

    With an increasing variety of biomarkers available for disease detection, combining biomarkers into integrated multianalyte assays would theoretically increase the statistical power of the analysis, if overfitting is appropriately protected against. There have been a number of attempts that use AI or ML to combine multiple types of cfDNA features (Peneder et al. 2021; Siejka-Zielińska et al. 2021; Lee et al. 2022b; Bae et al. 2023; Bie et al. 2023; Nguyen et al. 2023; Pham et al. 2023; Li et al. 2024; Moldovan et al. 2024; Wong et al. 2024; Liu et al. 2024a) or integrate cfDNA and protein analysis (Cohen et al. 2018; Douville et al. 2024). New developments in multimodal AI (Baltrušaitis et al. 2019) are moving beyond biochemical analytes to imaging, histopathology (Chen et al. 2022b; Haque et al. 2023), and clinical data (Vale-Silva and Rohr 2021; Tong et al. 2022; Peng et al. 2023). Indeed, clinical data can even be collected and inferred from interactive conversations using LLM-based chatbots (Peng et al. 2023). We eagerly await this holistic approach to cfDNA-based diagnostics, especially with the rise of transformer architectures in AI (Vaswani et al. 2017), which can be the basis of a general model architecture for all modalities (Lu et al. 2021; Acosta et al. 2022). It must, however, be emphasized again that transformers require even larger amounts of data than classical deep learning algorithms for them to be a meaningful and robust improvement.

    Improvements in our understanding of biological processes governing the cfDNA epigenetic and fragmentomic landscape, coupled with recent advancements in sequencing technologies, have given rise to a number of invaluable molecular features for liquid biopsies in oncology, pregnancy, organ transplantation, and immune diseases. ML and AI are powerful tools to leverage such features in high-dimensional space and produce robust predictions for diagnosis and prognosis. With the ever-expanding body of sequencing data available, researchers are increasingly exploring highly adaptable and multimodal AI frameworks for cfDNA-based diagnostics. These frameworks hold immense promise for enhancing our ability to detect various diseases at their early stages, making it possible to revolutionize precision medicine.

    Previous SectionNext Section

    Competing interest statement

    Y.M.D.L. holds equities in DRA, Take2, and Insighta. P.J. holds equities in Illumina. P.J. is a Director of DRA, KingMed Future, Take2, and Insighta. P.J. and Y.M.D.L. have filed a number of patents or patent applications related to liquid biopsies.

    Previous SectionNext Section

    Acknowledgments

    This study was supported by the Innovation and Technology Commission of the Hong Kong SAR Government (InnoHK initiative). Y.M.D.L. received an endowed chair from the Li Ka Shing Foundation.

    Previous SectionNext Section

    Footnotes

    This article, published in Genome Research, is available under a Creative Commons License (Attribution-NonCommercial 4.0 International), as described at http://creativecommons.org/licenses/by-nc/4.0/.

    Previous Section
     

    References

    1. ↵
      Abbosh C, Frankell AM, Harrison T, Kisistok J, Garnett A, Johnson L, Veeriah S, Moreau M, Chesh A, Chaunzwa TL, et al. 2023. Tracking early lung cancer metastatic dissemination in TRACERx using ctDNA. Nature 616: 553–562. doi:10.1038/s41586-023-05776-4
      CrossRefMedlineGoogle Scholar
    2. ↵
      Abramson J, Adler J, Dunger J, Evans R, Green T, Pritzel A, Ronneberger O, Willmore L, Ballard AJ, Bambrick J, et al. 2024. Accurate structure prediction of biomolecular interactions with AlphaFold 3. Nature 630: 493–500. doi:10.1038/s41586-024-07487-w
      CrossRefMedlineGoogle Scholar
    3. ↵
      Abu-Mostafa YS, Magdon-Ismail M, Lin H-T. 2012. Learning from data. AMLBook, New York.
      Google Scholar
    4. ↵
      Acosta JN, Falcone GJ, Rajpurkar P, Topol EJ. 2022. Multimodal biomedical AI. Nat Med 28: 1773–1784. doi:10.1038/s41591-022-01981-2
      CrossRefMedlineGoogle Scholar
    5. ↵
      Alexandrov LB, Kim J, Haradhvala NJ, Huang MN, Tian Ng AW, Wu Y, Boot A, Covington KR, Gordenin DA, Bergstrom EN, et al. 2020. The repertoire of mutational signatures in human cancer. Nature 578: 94–101. doi:10.1038/s41586-020-1943-3
      CrossRefMedlineGoogle Scholar
    6. ↵
      Alford B, Landry BP, Hou S, Bower X, Bueno AM, Chen D, Husic B, Cantonwine DE, McElrath TF, Carozza JA, et al. 2023. Validation of a non-invasive prenatal test for fetal RhD, C, c, E, K and Fya antigens. Sci Rep 13: 12786. doi:10.1038/s41598-023-39283-3
      CrossRefMedlineGoogle Scholar
    7. ↵
      Alloghani M, Al-Jumeily D, Mustafina J, Hussain A, Aljaaf AJ. 2020. A systematic review on supervised and unsupervised machine learning algorithms for data science. In Supervised and unsupervised learning for data science (ed. Berry MW, et al.), pp. 3–21. Springer International Publishing, Cham, Switzerland.
      Google Scholar
    8. ↵
      Al-Mayouf SM, Sunker A, Abdwani R, Abrawi SA, Almurshedi F, Alhashmi N, Al Sonbul A, Sewairi W, Qari A, Abdallah E, et al. 2011. Loss-of-function variant in DNASE1L3 causes a familial form of systemic lupus erythematosus. Nat Genet 43: 1186–1188. doi:10.1038/ng.975
      CrossRefMedlineGoogle Scholar
    9. ↵
      Altman N, Krzywinski M. 2018. The curse(s) of dimensionality. Nat Methods 15: 399–400. doi:10.1038/s41592-018-0019-x
      CrossRefMedlineGoogle Scholar
    10. ↵
      Alwosheel A, van Cranenburgh S, Chorus CG. 2018. Is your dataset big enough? sample size requirements when using artificial neural networks for discrete choice analysis. J Choice Model 28: 167–182. doi:10.1016/j.jocm.2018.07.002
      CrossRefGoogle Scholar
    11. ↵
      Annapragada AV, Niknafs N, White JR, Bruhm DC, Cherry C, Medina JE, Adleff V, Hruban C, Mathios D, Foda ZH, et al. 2024. Genome-wide repeat landscapes in cancer and cell-free DNA. Sci Transl Med 16: eadj9283. doi:10.1126/scitranslmed.adj9283
      CrossRefMedlineGoogle Scholar
    12. ↵
      Arlot S, Celisse A. 2010. A survey of cross-validation procedures for model selection. Stat Surv 4: 40–79. doi:10.1214/09-SS054
      CrossRefGoogle Scholar
    13. ↵
      Bae M, Kim G, Lee T-R, Ahn JM, Park H, Park SR, Song KB, Jun E, Oh D, Lee J-W, et al. 2023. Integrative modeling of tumor genomes and epigenomes for enhanced cancer diagnosis by cell-free DNA. Nat Commun 14: 2017. doi:10.1038/s41467-023-37768-3
      CrossRefMedlineGoogle Scholar
    14. ↵
      Baltrušaitis T, Ahuja C, Morency L-P. 2019. Multimodal machine learning: a survey and taxonomy. IEEE Trans Pattern Anal Mach Intell 41: 423–443. doi:10.1109/TPAMI.2018.2798607
      CrossRefMedlineGoogle Scholar
    15. ↵
      Barreñada L, Dhiman P, Timmerman D, Boulesteix A-L, Van Calster B. 2024. Understanding overfitting in random forest for probability estimation: a visualization and simulation study. Diagn Progn Res 8: 14. doi:10.1186/s41512-024-00177-1
      CrossRefMedlineGoogle Scholar
    16. ↵
      Bartlett PL, Long PM, Lugosi G, Tsigler A. 2020. Benign overfitting in linear regression. Proc Natl Acad Sci 117: 30063–30070. doi:10.1073/pnas.1907378117
      Abstract/FREE Full Text
    17. ↵
      Becking EC, Linthorst J, Patton S, Gutowska-Ding W, Goodall R, Khawaja F, Morgan F, Deans Z, Chitty LS, Bekker MN, et al. 2023. Variability in fetal fraction estimation: comparing fetal fractions reported by noninvasive prenatal testing providers globally. Clin Chem 69: 160–167. doi:10.1093/clinchem/hvac207
      CrossRefMedlineGoogle Scholar
    18. ↵
      Bellman RE. 1961. Adaptive control processes: a guided tour. In Adaptive control processes. Princeton University Press, Princeton, NJ.
      Google Scholar
    19. ↵
      Biau G, Scornet E. 2016. A random forest guided tour. Test 25: 197–227. doi:10.1007/s11749-016-0481-7
      CrossRefGoogle Scholar
    20. ↵
      Bie F, Wang Z, Li Y, Guo W, Hong Y, Han T, Lv F, Yang S, Li S, Li X, et al. 2023. Multimodal analysis of cell-free DNA whole-methylome sequencing for cancer detection and localization. Nat Commun 14: 6042. doi:10.1038/s41467-023-41774-w
      CrossRefGoogle Scholar
    21. ↵
      Bishop CM. 1995. Neural networks for pattern recognition. Oxford University Press, New York.
      Google Scholar
    22. ↵
      Boža V, Brejová B, Vinař T. 2017. DeepNano: deep recurrent neural networks for base calling in MinION nanopore reads. PLoS One 12: e0178751. doi:10.1371/journal.pone.0178751
      CrossRefMedlineGoogle Scholar
    23. ↵
      Brandes N, Goldman G, Wang CH, Ye CJ, Ntranos V. 2023. Genome-wide prediction of disease variant effects with a deep protein language model. Nat Genet 55: 1512–1522. doi:10.1038/s41588-023-01465-0
      CrossRefGoogle Scholar
    24. ↵
      Brash DE. 2015. UV signature mutations. Photochem Photobiol 91: 15–26. doi:10.1111/php.12377
      CrossRefMedlineGoogle Scholar
    25. ↵
      Breiman L. 2001. Random forests. Mach Learn 45: 5–32. doi:10.1023/A:1010933404324
      CrossRefGoogle Scholar
    26. ↵
      Breiman L, Spector P. 1992. Submodel selection and evaluation in regression: the X-random case. Int Stat Rev Rev Int Stat 60: 291–319. doi:10.2307/1403680
      CrossRefGoogle Scholar
    27. ↵
      Brown T, Mann B, Ryder N, Subbiah M, Kaplan JD, Dhariwal P, Neelakantan A, Shyam P, Sastry G, Askell A, et al. 2020. Language models are few-shot learners. In Advances in neural information processing systems (ed. Larochelle H, et al.), Vol. 33, pp. 1877–1901. Curran Associates, Inc., New York. https://proceedings.neurips.cc/paper_files/paper/2020/file/1457c0d6bfcb4967418bfb8ac142f64a-Paper.pdf.
      Google Scholar
    28. ↵
      Bu L, Gupta G, Pai A, Anand S, Stites E, Moinuddin I, Bowers V, Jain P, Axelrod DA, Weir MR, et al. 2022. Clinical outcomes from the assessing donor-derived cell-free DNA monitoring insights of kidney allografts with longitudinal surveillance (ADMIRAL) study. Kidney Int 101: 793–803. doi:10.1016/j.kint.2021.11.034
      CrossRefMedlineGoogle Scholar
    29. ↵
      Chabon JJ, Hamilton EG, Kurtz DM, Esfahani MS, Moding EJ, Stehr H, Schroers-Martin J, Nabet BY, Chen B, Chaudhuri AA, et al. 2020. Integrating genomic features for non-invasive early lung cancer detection. Nature 580: 245–251. doi:10.1038/s41586-020-2140-0
      CrossRefMedlineGoogle Scholar
    30. ↵
      Chan KCA, Zhang J, Hui ABY, Wong N, Lau TK, Leung TN, Lo K-W, Huang DWS, Lo YMD. 2004. Size distributions of maternal and fetal DNA in maternal plasma. Clin Chem 50: 88–92. doi:10.1373/clinchem.2003.024893
      Abstract/FREE Full Text
    31. ↵
      Chan KCA, Jiang P, Sun K, Cheng YKY, Tong YK, Cheng SH, Wong AIC, Hudecova I, Leung TY, Chiu RWK, et al. 2016. Second generation noninvasive fetal genome analysis reveals de novo mutations, single-base parental inheritance, and preferred DNA ends. Proc Natl Acad Sci 113: E8159–E8168. doi:10.1073/pnas.1615800113
      Abstract/FREE Full Text
    32. ↵
      Chan KCA, Chu SWI, Lo YMD. 2018. Ambient temperature and screening for nasopharyngeal cancer. N Engl J Med 378: 962–963. doi:10.1056/NEJMc1800433
      CrossRefMedlineGoogle Scholar
    33. ↵
      Chan A, Naarmann-de Vries IS, Scheitl CPM, Höbartner C, Dieterich C. 2024. Detecting m6A at single-molecular resolution via direct RNA sequencing and realistic training data. Nat Commun 15: 3323. doi:10.1038/s41467-024-47661-2
      CrossRefMedlineGoogle Scholar
    34. ↵
      Chandrananda D, Thorne NP, Bahlo M. 2015. High-resolution characterization of sequence signatures due to non-random cleavage of cell-free DNA. BMC Med Genomics 8: 29. doi:10.1186/s12920-015-0107-z
      CrossRefMedlineGoogle Scholar
    35. ↵
      Chen M, Chan RWY, Cheung PPH, Ni M, Wong DKL, Zhou Z, Ma M-JL, Huang L, Xu X, Lee W-S, et al. 2022a. Fragmentomics of urinary cell-free DNA in nuclease knockout mouse models. PLoS Genet 18: e1010262. doi:10.1371/journal.pgen.1010262
      CrossRefMedlineGoogle Scholar
    36. ↵
      Chen RJ, Lu MY, Williamson DFK, Chen TY, Lipkova J, Noor Z, Shaban M, Shady M, Williams M, Joo B, et al. 2022b. Pan-cancer integrative histology-genomic analysis via multimodal deep learning. Cancer Cell 40: 865–878.e6. doi:10.1016/j.ccell.2022.07.004
      CrossRefMedlineGoogle Scholar
    37. ↵
      Cheng AP, Cheng MP, Loy CJ, Lenz JS, Chen K, Smalling S, Burnham P, Timblin KM, Orejas JL, Silverman E, et al. 2022. Cell-free DNA profiling informs all major complications of hematopoietic cell transplantation. Proc Natl Acad Sci 119: e2113476118. doi:10.1073/pnas.2113476118
      Abstract/FREE Full Text
    38. ↵
      Chernick MR, LaBudde RA. 2014. An introduction to bootstrap methods with applications to R. John Wiley & Sons, Hoboken, NJ.
      Google Scholar
    39. ↵
      Chiu RWK, Chan KCA, Gao Y, Lau VYM, Zheng W, Leung TY, Foo CHF, Xie B, Tsui NBY, Lun FMF, et al. 2008. Noninvasive prenatal diagnosis of fetal chromosomal aneuploidy by massively parallel genomic sequencing of DNA in maternal plasma. Proc Natl Acad Sci 105: 20458–20463. doi:10.1073/pnas.0810641105
      Abstract/FREE Full Text
    40. ↵
      Chiu RWK, Cantor CR, Lo YMD. 2009. Non-invasive prenatal diagnosis by single molecule counting technologies. Trends Genet 25: 324–331. doi:10.1016/j.tig.2009.05.004
      CrossRefMedlineGoogle Scholar
    41. ↵
      Chiu RWK, Akolekar R, Zheng YWL, Leung TY, Sun H, Chan KCA, Lun FMF, Go ATJI, Lau ET, To WWK, et al. 2011. Non-invasive prenatal assessment of trisomy 21 by multiplexed maternal plasma DNA sequencing: large scale validity study. BMJ 342: c7401. doi:10.1136/bmj.c7401
      Abstract/FREE Full Text
    42. ↵
      Chowdhury R, Bouatta N, Biswas S, Floristean C, Kharkar A, Roy K, Rochereau C, Ahdritz G, Zhang J, Church GM, et al. 2022. Single-sequence protein structure prediction using a language model and deep learning. Nat Biotechnol 40: 1617–1623. doi:10.1038/s41587-022-01432-w
      CrossRefMedlineGoogle Scholar
    43. ↵
      Choy LYL, Peng W, Jiang P, Cheng SH, Yu SCY, Shang H, Olivia Tse OY, Wong J, Wong VWS, Wong GLH, et al. 2022. Single-molecule sequencing enables long cell-free DNA detection and direct methylation analysis for cancer patients. Clin Chem 68: 1151–1163. doi:10.1093/clinchem/hvac086
      CrossRefMedlineGoogle Scholar
    44. ↵
      Christensen MH, Drue SO, Rasmussen MH, Frydendahl A, Lyskjær I, Demuth C, Nors J, Gotschalck KA, Iversen LH, Andersen CL, et al. 2023. DREAMS: deep read-level error model for sequencing data applied to low-frequency variant calling and circulating tumor DNA detection. Genome Biol 24: 99. doi:10.1186/s13059-023-02920-1
      CrossRefGoogle Scholar
    45. ↵
      Ciampiconi L, Elwood A, Leonardi M, Mohamed A, Rozza A. 2023. A survey and taxonomy of loss functions in machine learning. arXiv:2301.05579 [cs.LG]. doi:10.48550/arXiv.2301.05579
      CrossRefGoogle Scholar
    46. ↵
      Clark TA, Lu X, Luong K, Dai Q, Boitano M, Turner SW, He C, Korlach J. 2013. Enhanced 5-methylcytosine detection in single-molecule, real-time sequencing via Tet1 oxidation. BMC Biol 11: 4. doi:10.1186/1741-7007-11-4
      CrossRefMedlineGoogle Scholar
    47. ↵
      Cohen JD, Li L, Wang Y, Thoburn C, Afsari B, Danilova L, Douville C, Javed AA, Wong F, Mattox A, et al. 2018. Detection and localization of surgically resectable cancers with a multi-analyte blood test. Science 359: 926–930. doi:10.1126/science.aar3247
      Abstract/FREE Full Text
    48. ↵
      Conway A-M, Pearce SP, Clipson A, Hill SM, Chemi F, Slane-Tan D, Ferdous S, Hossain ASMM, Kamieniecka K, White DJ, et al. 2024. A cfDNA methylation-based tissue-of-origin classifier for cancers of unknown primary. Nat Commun 15: 3292. doi:10.1038/s41467-024-47195-7
      CrossRefMedlineGoogle Scholar
    49. ↵
      Costa J-M, Benachi A, Gautier E. 2002. New strategy for prenatal diagnosis of X-linked disorders. N Engl J Med 346: 1502–1502. doi:10.1056/NEJM200205093461918
      CrossRefMedlineGoogle Scholar
    50. ↵
      Cristiano S, Leal A, Phallen J, Fiksel J, Adleff V, Bruhm DC, Jensen SØ, Medina JE, Hruban C, White JR, et al. 2019. Genome-wide cell-free DNA fragmentation in patients with cancer. Nature 570: 385–389. doi:10.1038/s41586-019-1272-6
      CrossRefMedlineGoogle Scholar
    51. ↵
      Dar P, Jacobsson B, Clifton R, Egbert M, Malone F, Wapner RJ, Roman AS, Khalil A, Faro R, Madankumar R, et al. 2022a. Cell-free DNA screening for prenatal detection of 22q11.2 deletion syndrome. Am J Obstet Gynecol 227: 79.e1–79.e11. doi:10.1016/j.ajog.2022.01.002
      CrossRefMedlineGoogle Scholar
    52. ↵
      Dar P, Jacobsson B, MacPherson C, Egbert M, Malone F, Wapner RJ, Roman AS, Khalil A, Faro R, Madankumar R, et al. 2022b. Cell-free DNA screening for trisomies 21, 18, and 13 in pregnancies at low and high risk for aneuploidy with genetic confirmation. Am J Obstet Gynecol 227: 259.e1–259.e14. doi:10.1016/j.ajog.2022.01.019
      CrossRefMedlineGoogle Scholar
    53. ↵
      Deignan JL, Chao E, Gannon JL, Greely HT, Hagman KDF, Mao R, Topper S. 2020. Points to consider when assessing relationships (or suspecting misattributed relationships) during family-based clinical genomic testing: a statement of the American college of medical genetics and genomics (ACMG). Genet Med 22: 1285–1287. doi:10.1038/s41436-020-0821-6
      CrossRefMedlineGoogle Scholar
    54. ↵
      de Santana Correia A, Colombini EL. 2022. Attention, please! a survey of neural attention models in deep learning. Artif Intell Rev 55: 6037–6124. doi:10.1007/s10462-022-10148-x
      CrossRefGoogle Scholar
    55. ↵
      De Vlaminck I, Valantine HA, Snyder TM, Strehl C, Cohen G, Luikart H, Neff NF, Okamoto J, Bernstein D, Weisshaar D, et al. 2014. Circulating cell-free DNA enables noninvasive diagnosis of heart transplant rejection. Sci Transl Med 6: 241ra77–241ra77. doi:10.1126/scitranslmed.3007803
      Abstract/FREE Full Text
    56. ↵
      Dietterich TG. 2000. Ensemble methods in machine learning. In Multiple classifier systems, lecture notes in computer science, pp. 1–15. Springer, Berlin.
      Google Scholar
    57. ↵
      Ding SC, Chan RWY, Peng W, Huang L, Zhou Z, Hu X, Volpi S, Hiraki LT, Vaglio A, Fenaroli P, et al. 2022. Jagged ends on multinucleosomal cell-free DNA serve as a biomarker for nuclease activity and systemic lupus erythematosus. Clin Chem 68: 917–926. doi:10.1093/clinchem/hvac050
      CrossRefMedlineGoogle Scholar
    58. ↵
      Douville C, Lahouel K, Kuo A, Grant H, Avigdor BE, Curtis SD, Summers M, Cohen JD, Wang Y, Mattox A, et al. 2024. Machine learning to detect the SINEs of cancer. Sci Transl Med 16: eadi3883. doi:10.1126/scitranslmed.adi3883
      CrossRefGoogle Scholar
    59. ↵
      Efron B. 1979. Bootstrap methods: another look at the jackknife. Ann Stat 7: 1–26. doi:10.1214/aos/1176344552
      CrossRefGoogle Scholar
    60. ↵
      Efron B, Hastie T. 2016. Computer age statistical inference: algorithms, evidence, and data science. Cambridge University Press, Cambridge.
      Google Scholar
    61. ↵
      Emmert-Streib F, Dehmer M. 2019. High-dimensional LASSO-based computational regression models: regularization, shrinkage, and selection. Mach Learn Knowl Extr 1: 359–383. doi:10.3390/make1010021
      CrossRefGoogle Scholar
    62. ↵
      Esfahani MS, Hamilton EG, Mehrmohamadi M, Nabet BY, Alig SK, King DA, Steen CB, Macaulay CW, Schultz A, Nesselbush MC, et al. 2022. Inferring gene expression from cell-free DNA fragmentation profiles. Nat Biotechnol 40: 585–597. doi:10.1038/s41587-022-01222-4
      CrossRefGoogle Scholar
    63. ↵
      Fan HC, Blumenfeld YJ, Chitkara U, Hudgins L, Quake SR. 2008. Noninvasive diagnosis of fetal aneuploidy by shotgun sequencing DNA from maternal blood. Proc Natl Acad Sci 105: 16266–16271. doi:10.1073/pnas.0808319105
      Abstract/FREE Full Text
    64. ↵
      Fan HC, Gu W, Wang J, Blumenfeld YJ, El-Sayed YY, Quake SR. 2012. Non-invasive prenatal measurement of the fetal genome. Nature 487: 320–324. doi:10.1038/nature11251
      CrossRefMedlineGoogle Scholar
    65. ↵
      Fedyuk V, Erez N, Furth N, Beresh O, Andreishcheva E, Shinde A, Jones D, Zakai BB, Mavor Y, Peretz T, et al. 2023. Multiplexed, single-molecule, epigenetic analysis of plasma-isolated nucleosomes for cancer diagnostics. Nat Biotechnol 41: 212–221. doi:10.1038/s41587-022-01447-3
      CrossRefGoogle Scholar
    66. ↵
      Finning K, Martin P, Summers J, Massey E, Poole G, Daniels G. 2008. Effect of high throughput RHD typing of fetal DNA in maternal plasma on use of anti-RhD immunoglobulin in RhD negative pregnant women: prospective feasibility study. BMJ 336: 816–818. doi:10.1136/bmj.39518.463206.25
      Abstract/FREE Full Text
    67. ↵
      Fiorentino F, Bono S, Pizzuti F, Mariano M, Polverari A, Duca S, Sessa M, Baldi M, Diano L, Spinella F. 2016. The importance of determining the limit of detection of non-invasive prenatal testing methods. Prenat Diagn 36: 304–311. doi:10.1002/pd.4780
      CrossRefMedlineGoogle Scholar
    68. ↵
      Foda ZH, Annapragada AV, Boyapati K, Bruhm DC, Vulpescu NA, Medina JE, Mathios D, Cristiano S, Niknafs N, Luu HT, et al. 2023. Detecting liver cancer using cell-free DNA fragmentomes. Cancer Discov 13: 616–631. doi:10.1158/2159-8290.CD-22-0659
      CrossRefGoogle Scholar
    69. ↵
      Forney GD. 1973. The viterbi algorithm. Proc IEEE 61: 268–278. doi:10.1109/PROC.1973.9030
      CrossRefGoogle Scholar
    70. ↵
      Forshew T, Murtaza M, Parkinson C, Gale D, Tsui DWY, Kaper F, Dawson S-J, Piskorz AM, Jimenez-Linan M, Bentley D, et al. 2012. Noninvasive identification and monitoring of cancer mutations by targeted deep sequencing of plasma DNA. Sci Transl Med 4: 136ra68. doi:10.1126/scitranslmed.3003726
      Abstract/FREE Full Text
    71. ↵
      Gao Q, Lin YP, Li BS, Wang GQ, Dong LQ, Shen BY, Lou WH, Wu WC, Ge D, Zhu QL, et al. 2023. Unintrusive multi-cancer detection by circulating cell-free DNA methylation sequencing (THUNDER): development and independent validation studies. Ann Oncol 34: 486–495. doi:10.1016/j.annonc.2023.02.010
      CrossRefMedlineGoogle Scholar
    72. ↵
      Gezer U, Yörüker EE, Keskin M, Kulle CB, Dharuman Y, Holdenrieder S. 2015. Histone methylation marks on circulating nucleosomes as novel blood-based biomarker in colorectal cancer. Int J Mol Sci 16: 29654–29662. doi:10.3390/ijms161226180
      CrossRefMedlineGoogle Scholar
    73. ↵
      Ghojogh B, Crowley M. 2023. The theory behind overfitting, cross validation, regularization, bagging, and boosting: tutorial. arXiv:1905.12787 [stat.ML]. doi:10.48550/arXiv.1905.12787
      CrossRefGoogle Scholar
    74. ↵
      Grabuschnig S, Bronkhorst AJ, Holdenrieder S, Rosales Rodriguez I, Schliep KP, Schwendenwein D, Ungerer V, Sensen CW. 2020. Putative origins of cell-free DNA in humans: a review of active and passive nucleic acid release mechanisms. Int J Mol Sci 21: 8062. doi:10.3390/ijms21218062
      CrossRefMedlineGoogle Scholar
    75. ↵
      Greener JG, Kandathil SM, Moffat L, Jones DT. 2022. A guide to machine learning for biologists. Nat Rev Mol Cell Biol 23: 40–55. doi:10.1038/s41580-021-00407-0
      CrossRefMedlineGoogle Scholar
    76. ↵
      Grumaz C, Hoffmann A, Vainshtein Y, Kopp M, Grumaz S, Stevens P, Decker SO, Weigand MA, Hofer S, Brenner T, et al. 2020. Rapid next-generation sequencing–based diagnostics of bacteremia in septic patients. J Mol Diagn 22: 405–418. doi:10.1016/j.jmoldx.2019.12.006
      CrossRefMedlineGoogle Scholar
    77. ↵
      Guo S, Diep D, Plongthongkum N, Fung H-L, Zhang K, Zhang K. 2017. Identification of methylation haplotype blocks aids in deconvolution of heterogeneous tissue samples and tumor tissue-of-origin mapping from plasma DNA. Nat Genet 49: 635–642. doi:10.1038/ng.3805
      CrossRefMedlineGoogle Scholar
    78. ↵
      Hahn MA, Li AX, Wu X, Pfeifer GP. 2015. Single base resolution analysis of 5-methylcytosine and 5-hydroxymethylcytosine by RRBS and TAB-RRBS. In Cancer epigenetics: risk assessment, diagnosis, treatment, and prognosis: methods in molecular biology (ed. Verma M), pp. 273–287. Springer, New York.
      Google Scholar
    79. ↵
      Hall M, van der Maaten L, Gustafson L, Jones M, Adcock A. 2022. A systematic study of bias amplification. arXiv:2201.11706 [cs.LG]. doi:10.48550/arXiv.2201.11706
      CrossRefGoogle Scholar
    80. ↵
      Han DSC, Lo YMD. 2021. The nexus of cfDNA and nuclease biology. Trends Genet 37: 758–770. doi:10.1016/j.tig.2021.04.005
      CrossRefMedlineGoogle Scholar
    81. ↵
      Han DSC, Ni M, Chan RWY, Chan VWH, Lui KO, Chiu RWK, Lo YMD. 2020. The biology of cell-free DNA fragmentation and the roles of DNASE1, DNASE1L3, and DFFB. Am J Hum Genet 106: 202–214. doi:10.1016/j.ajhg.2020.01.008
      CrossRefMedlineGoogle Scholar
    82. ↵
      Haque MIU, Mukherjee D, Stopka SA, Agar NYR, Hinkle J, Ovchinnikova OS. 2023. Deep learning on multimodal chemical and whole slide imaging data for predicting prostate cancer directly from tissue images. J Am Soc Mass Spectrom 34: 227–235. doi:10.1021/jasms.2c00254
      CrossRefMedlineGoogle Scholar
    83. ↵
      Hastie T, Tibshirani R, Friedman J. 2009. The elements of statistical learning. Springer, New York.
      Google Scholar
    84. ↵
      Hestand MS, Bessem M, van Rijn P, de Menezes RX, Sie D, Bakker I, Boon EMJ, Sistermans EA, Weiss MM. 2019. Fetal fraction evaluation in non-invasive prenatal screening (NIPS). Eur J Hum Genet 27: 198–202. doi:10.1038/s41431-018-0271-7
      CrossRefMedlineGoogle Scholar
    85. ↵
      Hoerl AE, Kennard RW. 1970. Ridge regression: biased estimation for nonorthogonal problems. Technometrics 12: 55–67. doi:10.1080/00401706.1970.10488634
      CrossRefGoogle Scholar
    86. ↵
      Hoffmann CH. 2022. Is AI intelligent? an assessment of artificial intelligence, 70 years after turing. Technol Soc 68: 101893. doi:10.1016/j.techsoc.2022.101893
      CrossRefGoogle Scholar
    87. ↵
      Hou Y, Yang J, Qi Y, Guo F, Peng H, Wang D, Wang Y, Luo X, Li Y, Yin A. 2019. Factors affecting cell-free DNA fetal fraction: statistical analysis of 13,661 maternal plasmas for non-invasive prenatal screening. Hum Genomics 13: 62. doi:10.1186/s40246-019-0244-0
      CrossRefMedlineGoogle Scholar
    88. ↵
      Jacob DR, Guiblet WM, Mamayusupova H, Shtumpf M, Ciuta I, Ruje L, Gretton S, Bikova M, Correa C, Dellow E, et al. 2024. Nucleosome reorganisation in breast cancer tissues. Clin Epigenetics 16: 50. doi:10.1186/s13148-024-01656-4
      CrossRefMedlineGoogle Scholar
    89. ↵
      Jamshidi A, Liu MC, Klein EA, Venn O, Hubbell E, Beausang JF, Gross S, Melton C, Fields AP, Liu Q, et al. 2022. Evaluation of cell-free DNA approaches for multi-cancer early detection. Cancer Cell 40: 1537–1549.e12. doi:10.1016/j.ccell.2022.10.022
      CrossRefMedlineGoogle Scholar
    90. ↵
      Jia W, Sun M, Lian J, Hou S. 2022. Feature dimensionality reduction: a review. Complex Intell Syst 8: 2663–2693. doi:10.1007/s40747-021-00637-x
      CrossRefGoogle Scholar
    91. ↵
      Jiang P, Chan KCA, Liao GJW, Zheng YWL, Leung TY, Chiu RWK, Lo YMD, Sun H. 2012. Fetalquant: deducing fractional fetal DNA concentration from massively parallel sequencing of DNA in maternal plasma. Bioinformatics 28: 2883–2890. doi:10.1093/bioinformatics/bts549
      CrossRefMedlineGoogle Scholar
    92. ↵
      Jiang P, Chan CWM, Chan KCA, Cheng SH, Wong J, Wong VW-S, Wong GLH, Chan SL, Mok TSK, Chan HLY, et al. 2015. Lengthening and shortening of plasma DNA in hepatocellular carcinoma patients. Proc Natl Acad Sci 112: E1317–E1325. doi:10.1073/pnas.1500076112
      Abstract/FREE Full Text
    93. ↵
      Jiang P, Sun K, Tong YK, Cheng SH, Cheng THT, Heung MMS, Wong J, Wong VWS, Chan HLY, Chan KCA, et al. 2018. Preferred end coordinates and somatic variants as signatures of circulating tumor DNA associated with hepatocellular carcinoma. Proc Natl Acad Sci 115: E10925–E10933. doi:10.1073/pnas.1814616115
      Abstract/FREE Full Text
    94. ↵
      Jiang P, Sun K, Peng W, Cheng SH, Ni M, Yeung PC, Heung MMS, Xie T, Shang H, Zhou Z, et al. 2020a. Plasma DNA end-motif profiling as a fragmentomic marker in cancer, pregnancy, and transplantation. Cancer Discov 10: 664–673. doi:10.1158/2159-8290.CD-19-0622
      Abstract/FREE Full Text
    95. ↵
      Jiang P, Xie T, Ding SC, Zhou Z, Cheng SH, Chan RWY, Lee W-S, Peng W, Wong J, Wong VWS, et al. 2020b. Detection and characterization of jagged ends of double-stranded DNA in plasma. Genome Res 30: 1144–1153. doi:10.1101/gr.261396.120
      Abstract/FREE Full Text
    96. ↵
      Johnson SR, Fu X, Viknander S, Goldin C, Monaco S, Zelezniak A, Yang KK. 2024. Computational scoring and experimental evaluation of enzymes generated by neural networks. Nat Biotechnol doi:10.1038/s41587-024-02214-2
      CrossRefGoogle Scholar
    97. ↵
      Jumper J, Evans R, Pritzel A, Green T, Figurnov M, Ronneberger O, Tunyasuvunakool K, Bates R, Žídek A, Potapenko A, et al. 2021. Highly accurate protein structure prediction with AlphaFold. Nature 596: 583–589. doi:10.1038/s41586-021-03819-2
      CrossRefMedlineGoogle Scholar
    98. ↵
      Kang S, Li Q, Chen Q, Zhou Y, Park S, Lee G, Grimes B, Krysan K, Yu M, Wang W, et al. 2017. CancerLocator: non-invasive cancer diagnosis and tissue-of-origin prediction using methylation profiles of cell-free DNA. Genome Biol 18: 53. doi:10.1186/s13059-017-1191-5
      CrossRefMedlineGoogle Scholar
    99. ↵
      Kapoor S, Narayanan A. 2023. Leakage and the reproducibility crisis in machine-learning-based science. Patterns 4: 100804. doi:10.1016/j.patter.2023.100804
      CrossRefGoogle Scholar
    100. ↵
      Keller M, Agbor-Enoh S. 2021. Donor-derived cell-free DNA for acute rejection monitoring in heart and lung transplantation. Curr Transplant Rep 8: 351–358. doi:10.1007/s40472-021-00349-8
      CrossRefMedlineGoogle Scholar
    101. ↵
      Keller MB, Newman D, Alnababteh M, Ponor L, Shah P, Mathew J, Kong H, Andargie T, Park W, Charya A, et al. 2024. Extreme elevations of donor-derived cell-free DNA increases the risk of chronic lung allograft dysfunction and death, even without clinical manifestations of disease. J Heart Lung Transplant 43: 1374–1382. doi:10.1016/j.healun.2024.04.064
      CrossRefMedlineGoogle Scholar
    102. ↵
      Keyel PA. 2017. Dnases in health and disease. Dev Biol 429: 1–11. doi:10.1016/j.ydbio.2017.06.028
      CrossRefMedlineGoogle Scholar
    103. ↵
      Khush KK, De Vlaminck I, Luikart H, Ross DJ, Nicolls MR. 2021. Donor-derived, cell-free DNA levels by next-generation targeted sequencing are elevated in allograft rejection after lung transplantation. ERJ Open Res 7: 00462-2020. doi:10.1183/23120541.00462-2020
      Abstract/FREE Full Text
    104. ↵
      Kim SK, Hannum G, Geis J, Tynan J, Hogg G, Zhao C, Jensen TJ, Mazloom AR, Oeth P, Ehrich M, et al. 2015. Determination of fetal DNA fraction from the plasma of pregnant women using sequence read counts. Prenat Diagn 35: 810–815. doi:10.1002/pd.4615
      CrossRefMedlineGoogle Scholar
    105. ↵
      Kittles RA, Weiss KM. 2003. Race, ancestry, and genes: implications for defining disease risk. Annu Rev Genomics Hum Genet 4: 33–67. doi:10.1146/annurev.genom.4.070802.110356
      CrossRefMedlineGoogle Scholar
    106. ↵
      Kwapisz D. 2017. The first liquid biopsy test approved: Is it a new era of mutation testing for non-small cell lung cancer? Ann Transl Med 5: 46. doi:10.21037/atm.2017.01.32
      CrossRefMedlineGoogle Scholar
    107. ↵
      Kwon H-J, Yun S, Joo J, Park D, Do W-J, Lee S, Lee M-S. 2023. Improving the accuracy of noninvasive prenatal testing through size-selection between fetal and maternal cfDNA. Prenat Diagn 43: 1581–1592. doi:10.1002/pd.6464
      CrossRefMedlineGoogle Scholar
    108. ↵
      Lam K-WG, Jiang P, Liao GJW, Chan KCA, Leung TY, Chiu RWK, Lo YMD. 2012. Noninvasive prenatal diagnosis of monogenic diseases by targeted massively parallel sequencing of maternal plasma: application to β-thalassemia. Clin Chem 58: 1467–1475. doi:10.1373/clinchem.2012.189589
      Abstract/FREE Full Text
    109. ↵
      Lee DD, Seung HS. 1999. Learning the parts of objects by non-negative matrix factorization. Nature 401: 788–791. doi:10.1038/44565
      CrossRefMedlineGoogle Scholar
    110. ↵
      Lee J, Lee S-M, Ahn JM, Lee T-R, Kim W, Cho E-H, Ki C-S. 2022a. Development and performance evaluation of an artificial intelligence algorithm using cell-free DNA fragment distance for non-invasive prenatal testing (aiD-NIPT). Front Genet 13: 999587. doi:10.3389/fgene.2022.999587
      CrossRefMedlineGoogle Scholar
    111. ↵
      Lee J, Lee T-R, Kim G, Ahn JM, Park SR, Song K-B, Jun E, Oh D, Lee J-W, Park YS, et al. 2022b. 916P deep learning-based multimodal ensemble algorithm for multi-cancer detection and classification using cf-WGS. Ann Oncol 33: S965–S966. doi:10.1016/j.annonc.2022.07.1041
      CrossRefGoogle Scholar
    112. ↵
      Leek JT, Scharpf RB, Bravo HC, Simcha D, Langmead B, Johnson WE, Geman D, Baggerly K, Irizarry RA. 2010. Tackling the widespread and critical impact of batch effects in high-throughput data. Nat Rev Genet 11: 733–739. doi:10.1038/nrg2825
      CrossRefMedlineGoogle Scholar
    113. ↵
      Legler TJ, Lührig S, Korschineck I, Schwartz D. 2021. Diagnostic performance of the noninvasive prenatal FetoGnost RhD assay for the prediction of the fetal RhD blood group status. Arch Gynecol Obstet 304: 1191–1196. doi:10.1007/s00404-021-06055-1
      CrossRefMedlineGoogle Scholar
    114. ↵
      Li W, Li Q, Kang S, Same M, Zhou Y, Sun C, Liu C-C, Matsuoka L, Sher L, Wong WH, et al. 2018. CancerDetector: ultrasensitive and non-invasive cancer detection at the resolution of individual reads using cell-free DNA methylation sequencing data. Nucleic Acids Res 46: e89. doi:10.1093/nar/gky423
      CrossRefMedlineGoogle Scholar
    115. ↵
      Li J, Wei L, Zhang X, Zhang W, Wang H, Zhong B, Xie Z, Lv H, Wang X. 2021a. DISMIR: deep learning-based noninvasive cancer detection by integrating DNA sequence and methylation information of individual cell-free DNA reads. Brief Bioinform 22: bbab250. doi:10.1093/bib/bbab250
      CrossRefMedlineGoogle Scholar
    116. ↵
      Li S, Noor ZS, Zeng W, Stackpole ML, Ni X, Zhou Y, Yuan Z, Wong WH, Agopian VG, Dubinett SM, et al. 2021b. Sensitive detection of tumor mutations from blood and its application to immunotherapy prognosis. Nat Commun 12: 4172. doi:10.1038/s41467-021-24457-2
      CrossRefMedlineGoogle Scholar
    117. ↵
      Li X, Wang Y, Ruiz R. 2022. A survey on sparse learning models for feature selection. IEEE Trans Cybern 52: 1642–1660. doi:10.1109/TCYB.2020.2982445
      CrossRefMedlineGoogle Scholar
    118. ↵
      Li S, Hu R, Small C, Kang T-Y, Liu C-C, Zhou XJ, Li W. 2023a. cfSNV: a software tool for the sensitive detection of somatic mutations from cell-free DNA. Nat Protoc 18: 1563–1583. doi:10.1038/s41596-023-00807-w
      CrossRefMedlineGoogle Scholar
    119. ↵
      Li S, Zeng W, Ni X, Liu Q, Li W, Stackpole ML, Zhou Y, Gower A, Krysan K, Ahuja P, et al. 2023b. Comprehensive tissue deconvolution of cell-free DNA by deep learning for disease diagnosis and monitoring. Proc Natl Acad Sci 120: e2305236120. doi:10.1073/pnas.2305236120
      CrossRefMedlineGoogle Scholar
    120. ↵
      Li Y, Xu J, Chen C, Lu Z, Wan D, Li D, Li JS, Sorg AJ, Roberts CC, Mahajan S, et al. 2024. Multimodal epigenetic sequencing analysis (MESA) of cell-free DNA for non-invasive colorectal cancer detection. Genome Med 16: 9. doi:10.1186/s13073-023-01280-6
      CrossRefMedlineGoogle Scholar
    121. ↵
      Liang N, Li B, Jia Z, Wang C, Wu P, Zheng T, Wang Y, Qiu F, Wu Y, Su J, et al. 2021. Ultrasensitive detection of circulating tumour DNA via deep methylation sequencing aided by machine learning. Nat Biomed Eng 5: 586–599. doi:10.1038/s41551-021-00746-5
      CrossRefMedlineGoogle Scholar
    122. ↵
      Liang W-W, Lu RJ-H, Jayasinghe RG, Foltz SM, Porta-Pardo E, Geffen Y, Wendl MC, Lazcano R, Kolodziejczak I, Song Y, et al. 2023. Integrative multi-omic cancer profiling reveals DNA methylation patterns associated with therapeutic vulnerability and cell-of-origin. Cancer Cell 41: 1567–1585.e7. doi:10.1016/j.ccell.2023.07.013
      CrossRefMedlineGoogle Scholar
    123. ↵
      Lin T, Wang Y, Liu X, Qiu X. 2022. A survey of transformers. AI Open 3: 111–132. doi:10.1016/j.aiopen.2022.10.001
      CrossRefGoogle Scholar
    124. ↵
      Lin Z, Akin H, Rao R, Hie B, Zhu Z, Lu W, Smetanin N, Verkuil R, Kabeli O, Shmueli Y, et al. 2023. Evolutionary-scale prediction of atomic-level protein structure with a language model. Science 379: 1123–1130. doi:10.1126/science.ade2574
      CrossRefMedlineGoogle Scholar
    125. ↵
      Liu MC, Oxnard GR, Klein EA, Swanton C, Seiden MV, Liu MC, Oxnard GR, Klein EA, Smith D, Richards D, et al. 2020. Sensitive and specific multi-cancer detection and localization using methylation signatures in cell-free DNA. Ann Oncol 31: 745–759. doi:10.1016/j.annonc.2020.02.011
      CrossRefMedlineGoogle Scholar
    126. ↵
      Liu J, Dai L, Wang Q, Li C, Liu Z, Gong T, Xu H, Jia Z, Sun W, Wang X, et al. 2024a. Multimodal analysis of cfDNA methylomes for early detecting esophageal squamous cell carcinoma and precancerous lesions. Nat Commun 15: 3700. doi:10.1038/s41467-024-47886-1
      CrossRefMedlineGoogle Scholar
    127. ↵
      Liu Y, Reed SC, Lo C, Choudhury AD, Parsons HA, Stover DG, Ha G, Gydush G, Rhoades J, Rotem D, et al. 2024b. FinaleMe: predicting DNA methylation by the fragmentation patterns of plasma cell-free DNA. Nat Commun 15: 2790. doi:10.1038/s41467-024-47196-6
      CrossRefMedlineGoogle Scholar
    128. ↵
      Lo YMD, Corbetta N, Chamberlain PF, Rai V, Sargent IL, Redman CW, Wainscoat JS. 1997. Presence of fetal DNA in maternal plasma and serum. Lancet 350: 485–487. doi:10.1016/S0140-6736(97)02174-0
      CrossRefMedlineGoogle Scholar
    129. ↵
      Lo YD, Tein MS, Pang CC, Yeung CK, Tong K-L, Hjelm NM. 1998a. Presence of donor-specific DNA in plasma of kidney and liver-transplant recipients. Lancet 351: 1329–1330. doi:10.1016/S0140-6736(05)79055-3
      CrossRefMedlineGoogle Scholar
    130. ↵
      Lo YM, Tein MS, Lau TK, Haines CJ, Leung TN, Poon PM, Wainscoat JS, Johnson PJ, Chang AM, Hjelm NM. 1998b. Quantitative analysis of fetal DNA in maternal plasma and serum: implications for noninvasive prenatal diagnosis. Am J Hum Genet 62: 768–775. doi:10.1086/301800
      CrossRefMedlineGoogle Scholar
    131. ↵
      Lo YMD, Lun FMF, Chan KCA, Tsui NBY, Chong KC, Lau TK, Leung TY, Zee BCY, Cantor CR, Chiu RWK. 2007. Digital PCR for the molecular detection of fetal chromosomal aneuploidy. Proc Natl Acad Sci 104: 13116–13121. doi:10.1073/pnas.0705765104
      Abstract/FREE Full Text
    132. ↵
      Lo YMD, Chan KCA, Sun H, Chen EZ, Jiang P, Lun FMF, Zheng YW, Leung TY, Lau TK, Cantor CR, et al. 2010. Maternal plasma DNA sequencing reveals the genome-wide genetic and mutational profile of the fetus. Sci Transl Med 2: 61ra91. doi:10.1126/scitranslmed.3001720
      Abstract/FREE Full Text
    133. ↵
      Lo YMD, Han DSC, Jiang P, Chiu RWK. 2021. Epigenetics, fragmentomics, and topology of cell-free DNA in liquid biopsies. Science 372: eaaw3616. doi:10.1126/science.aaw3616
      Abstract/FREE Full Text
    134. ↵
      Loyfer N, Magenheim J, Peretz A, Cann G, Bredno J, Klochendler A, Fox-Fisher I, Shabi-Porat S, Hecht M, Pelet T, et al. 2023. A DNA methylation atlas of normal human cell types. Nature 613: 355–364. doi:10.1038/s41586-022-05580-6
      CrossRefMedlineGoogle Scholar
    135. ↵
      Lu K, Grover A, Abbeel P, Mordatch I. 2021. Pretrained transformers as universal computation engines. arXiv:2103.05247 [cs.LG]. doi:10.48550/arXiv.2103.05247
      CrossRefGoogle Scholar
    136. ↵
      Lun FMF, Tsui NBY, Chan KCA, Leung TY, Lau TK, Charoenkwan P, Chow KCK, Lo WYW, Wanapirak C, Sanguansermsri T, et al. 2008. Noninvasive prenatal diagnosis of monogenic diseases by digital size selection and relative mutation dosage on DNA in maternal plasma. Proc Natl Acad Sci 105: 19920–19925. doi:10.1073/pnas.0810373105
      Abstract/FREE Full Text
    137. ↵
      Lun FM, Chiu RW, Sun K, Leung TY, Jiang P, Chan KA, Sun H, Lo YD. 2013. Noninvasive prenatal methylomic analysis by genomewide bisulfite sequencing of maternal plasma DNA. Clin Chem 59: 1583–1594. doi:10.1373/clinchem.2013.212274
      Abstract/FREE Full Text
    138. ↵
      Luo H, Wei W, Ye Z, Zheng J, Xu R. 2021. Liquid biopsy of methylation biomarkers in cell-free DNA. Trends Mol Med 27: 482–500. doi:10.1016/j.molmed.2020.12.011
      CrossRefMedlineGoogle Scholar
    139. ↵
      Ma D, Ge H, Li X, Jiang T, Chen F, Zhang Y, Hu P, Chen S, Zhang J, Ji X, et al. 2014. Haplotype-based approach for noninvasive prenatal diagnosis of congenital adrenal hyperplasia by maternal plasma DNA sequencing. Gene 544: 252–258. doi:10.1016/j.gene.2014.04.055
      CrossRefMedlineGoogle Scholar
    140. ↵
      Mathios D, Johansen JS, Cristiano S, Medina JE, Phallen J, Larsen KR, Bruhm DC, Niknafs N, Ferreira L, Adleff V, et al. 2021. Detection and characterization of lung cancer using cell-free DNA fragmentomes. Nat Commun 12: 5060. doi:10.1038/s41467-021-24994-w
      CrossRefMedlineGoogle Scholar
    141. ↵
      McCulloch WS, Pitts W. 1943. A logical calculus of the ideas immanent in nervous activity. Bull Math Biophys 5: 115–133. doi:10.1007/BF02478259
      CrossRefGoogle Scholar
    142. ↵
      Mizuta R, Araki S, Furukawa M, Furukawa Y, Ebara S, Shiokawa D, Hayashi K, Tanuma S, Kitamura D. 2013. DNase γ is the effector endonuclease for internucleosomal DNA fragmentation in necrosis. PLoS One 8: e80223. doi:10.1371/journal.pone.0080223
      CrossRefMedlineGoogle Scholar
    143. ↵
      Mohan P, Lemoine J, Trotter C, Rakova I, Billings P, Peacock S, Kao C-Y, Wang Y, Xia F, Eng CM, et al. 2022. Clinical experience with non-invasive prenatal screening for single-gene disorders. Ultrasound Obstet Gynecol 59: 33–39. doi:10.1002/uog.23756
      CrossRefMedlineGoogle Scholar
    144. ↵
      Moldovan N, van der Pol Y, van den Ende T, Boers D, Verkuijlen S, Creemers A, Ramaker J, Vu T, Bootsma S, Lenos KJ, et al. 2024. Multi-modal cell-free DNA genomic and fragmentomic patterns enhance cancer survival and recurrence analysis. Cell Rep Med 5: 101349. doi:10.1016/j.xcrm.2023.101349
      CrossRefMedlineGoogle Scholar
    145. ↵
      Moss J, Magenheim J, Neiman D, Zemmour H, Loyfer N, Korach A, Samet Y, Maoz M, Druid H, Arner P, et al. 2018. Comprehensive human cell-type methylation atlas reveals origins of circulating cell-free DNA in health and disease. Nat Commun 9: 5068. doi:10.1038/s41467-018-07466-6
      CrossRefMedlineGoogle Scholar
    146. ↵
      Moss J, Ben-Ami R, Shai E, Gal-Rosenberg O, Kalish Y, Klochendler A, Cann G, Glaser B, Arad A, Shemer R, et al. 2023. Megakaryocyte- and erythroblast-specific cell-free DNA patterns in plasma and platelets reflect thrombopoiesis and erythropoiesis levels. Nat Commun 14: 7542. doi:10.1038/s41467-023-43310-2
      CrossRefMedlineGoogle Scholar
    147. ↵
      Mouliere F, Chandrananda D, Piskorz AM, Moore EK, Morris J, Ahlborn LB, Mair R, Goranova T, Marass F, Heider K, et al. 2018. Enhanced detection of circulating tumor DNA by fragment size analysis. Sci Transl Med 10: eaat4921. doi:10.1126/scitranslmed.aat4921
      Abstract/FREE Full Text
    148. ↵
      Mueller JP, Massaron L. 2021. Machine learning for dummies. John Wiley & Sons, Hoboken, NJ.
      Google Scholar
    149. ↵
      Muggleton S. 2014. Alan Turing and the development of artificial intelligence. AI Commun 27: 3–10. doi:10.3233/AIC-130579
      CrossRefGoogle Scholar
    150. ↵
      Murtaza M, Dawson S-J, Tsui DWY, Gale D, Forshew T, Piskorz AM, Parkinson C, Chin S-F, Kingsbury Z, Wong ASC, et al. 2013. Non-invasive analysis of acquired resistance to cancer therapy by sequencing of plasma DNA. Nature 497: 108–112. doi:10.1038/nature12065
      CrossRefMedlineGoogle Scholar
    151. ↵
      Napirei M, Karsunky H, Zevnik B, Stephan H, Mannherz HG, Möröy T. 2000. Features of systemic lupus erythematosus in Dnase1-deficient mice. Nat Genet 25: 177–181. doi:10.1038/76032
      CrossRefMedlineGoogle Scholar
    152. ↵
      Napirei M, Ludwig S, Mezrhab J, Klöckl T, Mannherz HG. 2009. Murine serum nucleases: contrasting effects of plasmin and heparin on the activities of DNase1 and DNase1-like 3 (DNase1l3). FEBS J 276: 1059–1073. doi:10.1111/j.1742-4658.2008.06849.x
      CrossRefMedlineGoogle Scholar
    153. ↵
      Nawroz H, Koch W, Anker P, Stroun M, Sidransky D. 1996. Microsatellite alterations in serum DNA of head and neck cancer patients. Nat Med 2: 1035–1037. doi:10.1038/nm0996-1035
      CrossRefMedlineGoogle Scholar
    154. ↵
      Neumann D, Reddy ASN, Ben-Hur A. 2022. RODAN: a fully convolutional architecture for basecalling nanopore RNA sequencing data. BMC Bioinformatics 23: 142. doi:10.1186/s12859-022-04686-y
      CrossRefMedlineGoogle Scholar
    155. ↵
      New MI, Tong YK, Yuen T, Jiang P, Pina C, Chan KCA, Khattab A, Liao GJW, Yau M, Kim S-M, et al. 2014. Noninvasive prenatal diagnosis of congenital adrenal hyperplasia using cell-free fetal DNA in maternal plasma. J Clin Endocrinol Metab 99: E1022–E1030. doi:10.1210/jc.2014-1118
      CrossRefMedlineGoogle Scholar
    156. ↵
      Newman AM, Lovejoy AF, Klass DM, Kurtz DM, Chabon JJ, Scherer F, Stehr H, Liu CL, Bratman SV, Say C, et al. 2016. Integrated digital error suppression for improved detection of circulating tumor DNA. Nat Biotechnol 34: 547–555. doi:10.1038/nbt.3520
      CrossRefMedlineGoogle Scholar
    157. ↵
      Nguyen VTC, Nguyen TH, Doan NNT, Pham TMQ, Nguyen GTH, Nguyen TD, Tran TTT, Vo DL, Phan TH, Jasmine TX, et al. 2023. Multimodal analysis of methylomics and fragmentomics in plasma cell-free DNA for multi-cancer early detection and localization. eLife 12: RP89083. doi:10.7554/eLife.89083.3
      CrossRefMedlineGoogle Scholar
    158. ↵
      Noll M. 1974. Internal structure of the chromatin subunit. Nucleic Acids Res 1: 1573–1578. doi:10.1093/nar/1.11.1573
      CrossRefMedlineGoogle Scholar
    159. ↵
      Norton ME, Brar H, Weiss J, Karimi A, Laurent LC, Caughey AB, Rodriguez MH, Williams J, Mitchell ME, Adair CD, et al. 2012. Non-invasive chromosomal evaluation (NICE) study: results of a multicenter prospective cohort study for detection of fetal trisomy 21 and trisomy 18. Am J Obstet Gynecol 207: 137.e1–137.e8. doi:10.1016/j.ajog.2012.05.021
      CrossRefMedlineGoogle Scholar
    160. ↵
      Oberhofer A, Bronkhorst AJ, Uhlig C, Ungerer V, Holdenrieder S. 2022. Tracing the origin of cell-free DNA molecules through tissue-specific epigenetic signatures. Diagnostics 12: 1834. doi:10.3390/diagnostics12081834
      CrossRefGoogle Scholar
    161. ↵
      Paluoja P, Teder H, Ardeshirdavani A, Bayindir B, Vermeesch J, Salumets A, Krjutškov K, Palta P. 2021. Systematic evaluation of NIPT aneuploidy detection software tools with clinically validated NIPT samples. PLoS Comput Biol 17: e1009684. doi:10.1371/journal.pcbi.1009684
      CrossRefMedlineGoogle Scholar
    162. ↵
      Pan Y, Pan X, Zhuang D, Zhou Y, Xue J, Wu S, Chen C, Li H. 2024. A statistical investigation of parameters associated with low cell-free fetal DNA fraction in maternal plasma for noninvasive prenatal testing. J Matern Fetal Neonatal Med 37: 2338440. doi:10.1080/14767058.2024.2338440
      CrossRefMedlineGoogle Scholar
    163. ↵
      Peneder P, Stütz AM, Surdez D, Krumbholz M, Semper S, Chicard M, Sheffield NC, Pierron G, Lapouble E, Tötzl M, et al. 2021. Multimodal analysis of cell-free DNA whole-genome sequencing for pediatric cancers with low mutational burden. Nat Commun 12: 3230. doi:10.1038/s41467-021-23445-w
      CrossRefMedlineGoogle Scholar
    164. ↵
      Peng Z, Ma R, Zhang Y, Yan M, Lu J, Cheng Q, Liao J, Zhang Y, Wang J, Zhao Y, et al. 2023. Development and evaluation of multimodal AI for diagnosis and triage of ophthalmic diseases using ChatGPT and anterior segment images: protocol for a two-stage cross-sectional study. Front Artif Intell 6: 1323924. doi:10.3389/frai.2023.1323924
      CrossRefMedlineGoogle Scholar
    165. ↵
      Pham TMQ, Phan TH, Jasmine TX, Tran TTT, Huynh LAK, Vo TL, Nai THT, Tran TT, Truong MH, Tran NC, et al. 2023. Multimodal analysis of genome-wide methylation, copy number aberrations, and end motif signatures enhances detection of early-stage breast cancer. Front Oncol 13: 1127086. doi:10.3389/fonc.2023.1127086
      CrossRefGoogle Scholar
    166. ↵
      Pulini AA, Kerr WT, Loo SK, Lenartowicz A. 2019. Classification accuracy of neuroimaging biomarkers in attention-deficit/hyperactivity disorder: effects of sample size and circular analysis. Biol Psychiatry Cogn Neurosci Neuroimaging 4: 108–120. doi:10.1016/j.bpsc.2018.06.003
      CrossRefMedlineGoogle Scholar
    167. ↵
      Raman L, Baetens M, De Smet M, Dheedene A, Van Dorpe J, Menten B. 2019. PREFACE: in silico pipeline for accurate cell-free fetal DNA fraction prediction. Prenat Diagn 39: 925–933. doi:10.1002/pd.5508
      CrossRefMedlineGoogle Scholar
    168. ↵
      Rang FJ, Kloosterman WP, de Ridder J. 2018. From squiggle to basepair: computational approaches for improving nanopore sequencing read accuracy. Genome Biol 19: 90. doi:10.1186/s13059-018-1462-9
      CrossRefMedlineGoogle Scholar
    169. ↵
      Renaud G, Nørgaard M, Lindberg J, Grönberg H, De Laere B, Jensen JB, Borre M, Andersen CL, Sørensen KD, Maretty L, et al. 2022. Unsupervised detection of fragment length signatures of circulating tumor DNA using non-negative matrix factorization. eLife 11: e71569. doi:10.7554/eLife.71569
      CrossRefMedlineGoogle Scholar
    170. ↵
      Rives A, Meier J, Sercu T, Goyal S, Lin Z, Liu J, Guo D, Ott M, Zitnick CL, Ma J, et al. 2021. Biological structure and function emerge from scaling unsupervised learning to 250 million protein sequences. Proc Natl Acad Sci 118: e2016239118. doi:10.1073/pnas.2016239118
      Abstract/FREE Full Text
    171. ↵
      Roberts DR, Bahn V, Ciuti S, Boyce MS, Elith J, Guillera-Arroita G, Hauenstein S, Lahoz-Monfort JJ, Schröder B, Thuiller W, et al. 2017. Cross-validation strategies for data with temporal, spatial, hierarchical, or phylogenetic structure. Ecography 40: 913–929. doi:10.1111/ecog.02881
      CrossRefGoogle Scholar
    172. ↵
      Rocke DM, Ideker T, Troyanskaya O, Quackenbush J, Dopazo J. 2009. Papers on normalization, variable selection, classification or clustering of microarray data. Bioinformatics 25: 701–702. doi:10.1093/bioinformatics/btp038
      CrossRefGoogle Scholar
    173. ↵
      Rosenblatt F. 1958. The perceptron: a probabilistic model for information storage and organization in the brain. Psychol Rev 65: 386–408. doi:10.1037/h0042519
      CrossRefMedlineGoogle Scholar
    174. ↵
      Sadeh R, Sharkia I, Fialkoff G, Rahat A, Gutin J, Chappleboim A, Nitzan M, Fox-Fisher I, Neiman D, Meler G, et al. 2021. ChIP-seq of plasma cell-free nucleosomes identifies gene expression programs of the cells of origin. Nat Biotechnol 39: 586–598. doi:10.1038/s41587-020-00775-6
      CrossRefGoogle Scholar
    175. ↵
      Schlaikjær Hartwig T, Ambye L, Gruhn JR, Petersen JF, Wrønding T, Amato L, Chi-Ho Chan A, Ji B, Bro-Jørgensen MH, Werge L, et al. 2023. Cell-free fetal DNA for genetic evaluation in Copenhagen Pregnancy Loss Study (COPL): a prospective cohort study. Lancet Lond Engl 401: 762–771. doi:10.1016/S0140-6736(22)02610-1
      CrossRefMedlineGoogle Scholar
    176. ↵
      Schütz E, Fischer A, Beck J, Harden M, Koch M, Wuensch T, Stockmann M, Nashan B, Kollmar O, Matthaei J, et al. 2017. Graft-derived cell-free DNA, a noninvasive early rejection and graft damage marker in liver transplantation: a prospective, observational, multicenter cohort study. PLoS Med 14: e1002286. doi:10.1371/journal.pmed.1002286
      CrossRefMedlineGoogle Scholar
    177. ↵
      Senior AW, Evans R, Jumper J, Kirkpatrick J, Sifre L, Green T, Qin C, Žídek A, Nelson AWR, Bridgland A, et al. 2019. Protein structure prediction using multiple deep neural networks in the 13th critical assessment of protein structure prediction (CASP13). Proteins Struct Funct Bioinforma 87: 1141–1148. doi:10.1002/prot.25834
      CrossRefMedlineGoogle Scholar
    178. ↵
      Senior AW, Evans R, Jumper J, Kirkpatrick J, Sifre L, Green T, Qin C, Žídek A, Nelson AWR, Bridgland A, et al. 2020. Improved protein structure prediction using potentials from deep learning. Nature 577: 706–710. doi:10.1038/s41586-019-1923-7
      CrossRefMedlineGoogle Scholar
    179. ↵
      Serpas L, Chan RWY, Jiang P, Ni M, Sun K, Rashidfarrokhi A, Soni C, Sisirak V, Lee W-S, Cheng SH, et al. 2019. Dnase1l3 deletion causes aberrations in length and end-motif frequencies in plasma DNA. Proc Natl Acad Sci 116: 641–649. doi:10.1073/pnas.1815031116
      Abstract/FREE Full Text
    180. ↵
      Shen SY, Singhania R, Fehringer G, Chakravarthy A, Roehrl MHA, Chadwick D, Zuzarte PC, Borgida A, Wang TT, Li T, et al. 2018. Sensitive tumour detection and classification using plasma cell-free DNA methylomes. Nature 563: 579–583. doi:10.1038/s41586-018-0703-0
      CrossRefMedlineGoogle Scholar
    181. ↵
      Shlien A, Malkin D. 2009. Copy number variations and cancer. Genome Med 1: 62. doi:10.1186/gm62
      CrossRefMedlineGoogle Scholar
    182. ↵
      Siejka-Zielińska P, Cheng J, Jackson F, Liu Y, Soonawalla Z, Reddy S, Silva M, Puta L, McCain MV, Culver EL, et al. 2021. Cell-free DNA TAPS provides multimodal information for early cancer detection. Sci Adv 7: eabh0534. doi:10.1126/sciadv.abh0534
      CrossRefMedlineGoogle Scholar
    183. ↵
      Sisirak V, Sally B, D'Agati V, Martinez-Ortiz W, Özçakar ZB, David J, Rashidfarrokhi A, Yeste A, Panea C, Chida AS, et al. 2016. Digestion of chromatin in apoptotic cell microparticles prevents autoimmunity. Cell 166: 88–101. doi:10.1016/j.cell.2016.05.034
      CrossRefMedlineGoogle Scholar
    184. ↵
      Smith ZD, Meissner A. 2013. DNA methylation: roles in mammalian development. Nat Rev Genet 14: 204–220. doi:10.1038/nrg3354
      CrossRefMedlineGoogle Scholar
    185. ↵
      Snyder MW, Kircher M, Hill AJ, Daza RM, Shendure J. 2016. Cell-free DNA comprises an in vivo nucleosome footprint that informs Its tissues-of-origin. Cell 164: 57–68. doi:10.1016/j.cell.2015.11.050
      CrossRefMedlineGoogle Scholar
    186. ↵
      Sohail M, Maier RM, Ganna A, Bloemendal A, Martin AR, Turchin MC, Chiang CW, Hirschhorn J, Daly MJ, Patterson N, et al. 2019. Polygenic adaptation on height is overestimated due to uncorrected stratification in genome-wide association studies. eLife 8: e39702. doi:10.7554/eLife.39702
      CrossRefMedlineGoogle Scholar
    187. ↵
      Sparks AB, Struble CA, Wang ET, Song K, Oliphant A. 2012. Noninvasive prenatal detection and selective analysis of cell-free DNA obtained from maternal blood: evaluation for trisomy 21 and trisomy 18. Am J Obstet Gynecol 206: 319.e1–319.e9. doi:10.1016/j.ajog.2012.01.030
      CrossRefMedlineGoogle Scholar
    188. ↵
      Srinivasan A, Bianchi DW, Huang H, Sehnert AJ, Rava RP. 2013. Noninvasive detection of fetal subchromosome abnormalities via deep sequencing of maternal plasma. Am J Hum Genet 92: 167–176. doi:10.1016/j.ajhg.2012.12.006
      CrossRefMedlineGoogle Scholar
    189. ↵
      Stackpole ML, Zeng W, Li S, Liu C-C, Zhou Y, He S, Yeh A, Wang Z, Sun F, Li Q, et al. 2022. Cost-effective methylome sequencing of cell-free DNA for accurately detecting and locating cancer. Nat Commun 13: 5566. doi:10.1038/s41467-022-32995-6
      CrossRefMedlineGoogle Scholar
    190. ↵
      Straver R, Sistermans EA, Holstege H, Visser A, Oudejans CBM, Reinders MJT. 2014. WISECONDOR: detection of fetal aberrations from shallow sequencing maternal plasma based on a within-sample comparison scheme. Nucleic Acids Res 42: e31. doi:10.1093/nar/gkt992
      CrossRefMedlineGoogle Scholar
    191. ↵
      Straver R, Oudejans CBM, Sistermans EA, Reinders MJT. 2016. Calculating the fetal fraction for noninvasive prenatal testing based on genome-wide nucleosome profiles. Prenat Diagn 36: 614–621. doi:10.1002/pd.4816
      CrossRefMedlineGoogle Scholar
    192. ↵
      Stroun M, Anker P, Maurice P, Lyautey J, Lederrey C, Beljanski M. 1989. Neoplastic characteristics of the DNA found in the plasma of cancer patients. Oncology 46: 318–322. doi:10.1159/000226740
      CrossRefMedlineGoogle Scholar
    193. ↵
      Sun K, Jiang P, Chan KCA, Wong J, Cheng YKY, Liang RHS, Chan W, Ma ESK, Chan SL, Cheng SH, et al. 2015. Plasma DNA tissue mapping by genome-wide methylation sequencing for noninvasive prenatal, cancer, and transplantation assessments. Proc Natl Acad Sci 112: E5503–E5512. doi:10.1073/pnas.1508736112
      Abstract/FREE Full Text
    194. ↵
      Sun K, Jiang P, Cheng SH, Cheng THT, Wong J, Wong VWS, Ng SSM, Ma BBY, Leung TY, Chan SL, et al. 2019. Orientation-aware plasma cell-free DNA fragmentation analysis in open chromatin regions informs tissue of origin. Genome Res 29: 418–427. doi:10.1101/gr.242719.118
      Abstract/FREE Full Text
    195. ↵
      Sun S, Cao Z, Zhu H, Zhao J. 2020. A survey of optimization methods from a machine learning perspective. IEEE Trans Cybern 50: 3668–3681. doi:10.1109/TCYB.2019.2950779
      CrossRefMedlineGoogle Scholar
    196. ↵
      Sun X, Feng W, Cui P, Ruan R, Ma W, Han Z, Sun J, Pan Y, Zhu J, Zhong X, et al. 2022. Detection and monitoring of HBV-related hepatocellular carcinoma from plasma cfDNA fragmentation profiles. Genomics 114: 110502. doi:10.1016/j.ygeno.2022.110502
      CrossRefMedlineGoogle Scholar
    197. ↵
      Tang H, Quertermous T, Rodriguez B, Kardia SLR, Zhu X, Brown A, Pankow JS, Province MA, Hunt SC, Boerwinkle E, et al. 2005. Genetic structure, self-identified race/ethnicity, and confounding in case-control association studies. Am J Hum Genet 76: 268–275. doi:10.1086/427888
      CrossRefMedlineGoogle Scholar
    198. ↵
      Tay JK, Narasimhan B, Hastie T. 2023. Elastic net regularization paths for all generalized linear models. J Stat Softw 106: 1. doi:10.18637/jss.v106.i01
      CrossRefMedlineGoogle Scholar
    199. ↵
      Tibshirani R. 1996. Regression shrinkage and selection via the lasso. J R Stat Soc Ser B Methodol 58: 267–288. doi:10.1111/j.2517-6161.1996.tb02080.x
      CrossRefGoogle Scholar
    200. ↵
      Tong H, Sun J, Fang J, Zhang M, Liu H, Xia R, Zhou W, Liu K, Chen X. 2022. A machine learning model based on PET/CT radiomics and clinical characteristics predicts tumor immune profiles in non-small cell lung cancer: a retrospective multicohort study. Front Immunol 13: 859323. doi:10.3389/fimmu.2022.859323
      CrossRefMedlineGoogle Scholar
    201. ↵
      Tse OYO, Jiang P, Cheng SH, Peng W, Shang H, Wong J, Chan SL, Poon LCY, Leung TY, Chan KCA, et al. 2021. Genome-wide detection of cytosine methylation by single molecule real-time sequencing. Proc Natl Acad Sci 118: e2019768118. doi:10.1073/pnas.2019768118
      Abstract/FREE Full Text
    202. ↵
      Tsui NBY, Kadir RA, Chan KCA, Chi C, Mellars G, Tuddenham EG, Leung TY, Lau TK, Chiu RWK, Lo YMD. 2011. Noninvasive prenatal diagnosis of hemophilia by microfluidics digital PCR analysis of maternal plasma DNA. Blood 117: 3684–3691. doi:10.1182/blood-2010-10-310789
      Abstract/FREE Full Text
    203. ↵
      Turing AM. 1950. Computing machinery and intelligence. Mind 59: 433–460. doi:10.1093/mind/LIX.236.433
      CrossRefGoogle Scholar
    204. ↵
      Ulz P, Thallinger GG, Auer M, Graf R, Kashofer K, Jahn SW, Abete L, Pristauz G, Petru E, Geigl JB, et al. 2016. Inferring expressed genes by whole-genome sequencing of plasma DNA. Nat Genet 48: 1273–1278. doi:10.1038/ng.3648
      CrossRefMedlineGoogle Scholar
    205. ↵
      Underhill HR, Kitzman JO, Hellwig S, Welker NC, Daza R, Baker DN, Gligorich KM, Rostomily RC, Bronner MP, Shendure J. 2016. Fragment length of circulating tumor DNA. PLoS Genet 12: e1006162. doi:10.1371/journal.pgen.1006162
      CrossRefMedlineGoogle Scholar
    206. ↵
      Vale-Silva LA, Rohr K. 2021. Long-term cancer survival prediction using multimodal deep learning. Sci Rep 11: 13505. doi:10.1038/s41598-021-92799-4
      CrossRefMedlineGoogle Scholar
    207. ↵
      Van den Meersche K, Soetaert K, Oevelen DV. 2009. xsample(): an R function for sampling linear inverse problems. J Stat Softw 30: 1–15. doi:10.18637/jss.v030.c01
      CrossRefMedlineGoogle Scholar
    208. ↵
      van der Pol Y, Moldovan N, Verkuijlen S, Ramaker J, Boers D, Onstenk W, de Rooij J, Bahce I, Pegtel DM, Mouliere F. 2022. The effect of preanalytical and physiological variables on cell-free DNA fragmentation. Clin Chem 68: 803–813. doi:10.1093/clinchem/hvac029
      CrossRefMedlineGoogle Scholar
    209. ↵
      van der Vaart M, Semenov DV, Kuligina EV, Richter VA, Pretorius PJ. 2009. Characterisation of circulating DNA by parallel tagged sequencing on the 454 platform. Clin Chim Acta 409: 21–27. doi:10.1016/j.cca.2009.08.011
      CrossRefMedlineGoogle Scholar
    210. ↵
      Vaswani A, Shazeer N, Parmar N, Uszkoreit J, Jones L, Gomez AN, Kaiser Ł, Polosukhin I. 2017. Attention is all you need. In Proceedings of the 31st International Conference on Neural Information Processing Systems (ed. Guyon I, et al.), Vol. 30. Curran Associates, Inc., Red Hook, NY. https://proceedings.neurips.cc/paper_files/paper/2017/file/3f5ee243547dee91fbd053c1c4a845aa-Paper.pdf.
      Google Scholar
    211. ↵
      Viterbi A. 1967. Error bounds for convolutional codes and an asymptotically optimum decoding algorithm. IEEE Trans Inf Theory 13: 260–269. doi:10.1109/TIT.1967.1054010
      CrossRefGoogle Scholar
    212. ↵
      Wan JCM, Massie C, Garcia-Corbacho J, Mouliere F, Brenton JD, Caldas C, Pacey S, Baird R, Rosenfeld N. 2017. Liquid biopsies come of age: towards implementation of circulating tumour DNA. Nat Rev Cancer 17: 223–238. doi:10.1038/nrc.2017.7
      CrossRefMedlineGoogle Scholar
    213. ↵
      Wang E, Batey A, Struble C, Musci T, Song K, Oliphant A. 2013. Gestational age and maternal weight effects on fetal cell-free DNA in maternal plasma. Prenat Diagn 33: 662–666. doi:10.1002/pd.4119
      CrossRefMedlineGoogle Scholar
    214. ↵
      Whalen S, Schreiber J, Noble WS, Pollard KS. 2022. Navigating the pitfalls of applying machine learning in genomics. Nat Rev Genet 23: 169–181. doi:10.1038/s41576-021-00434-9
      CrossRefMedlineGoogle Scholar
    215. ↵
      Wick RR, Judd LM, Holt KE. 2019. Performance of neural network basecalling tools for Oxford Nanopore sequencing. Genome Biol 20: 129. doi:10.1186/s13059-019-1727-y
      CrossRefMedlineGoogle Scholar
    216. ↵
      Widlak P, Garrard WT. 2009. Roles of the major apoptotic nuclease-DNA fragmentation factor-in biology and disease. Cell Mol Life Sci 66: 263–274. doi:10.1007/s00018-008-8472-9
      CrossRefMedlineGoogle Scholar
    217. ↵
      Widman AJ, Shah M, Frydendahl A, Halmos D, Khamnei CC, Øgaard N, Rajagopalan S, Arora A, Deshpande A, Hooper WF, et al. 2024. Ultrasensitive plasma-based monitoring of tumor burden using machine-learning-guided signal enrichment. Nat Med 30: 1655–1666. doi:10.1038/s41591-024-03040-4
      CrossRefMedlineGoogle Scholar
    218. ↵
      Wong D, Luo P, Oldfield LE, Gong H, Brunga L, Rabinowicz R, Subasri V, Chan C, Downs T, Farncombe KM, et al. 2024. Early cancer detection in Li–Fraumeni syndrome with cell-free DNA. Cancer Discov 14: 104–119. doi:10.1158/2159-8290.CD-23-0456
      CrossRefMedlineGoogle Scholar
    219. ↵
      Wooldridge M. 2021. A brief history of artificial intelligence: what it is, where we are, and where we are going. Flatiron Books, New York.
      Google Scholar
    220. ↵
      Wu X, Guo D, Li Y, Xie X, Su L, Cai M, Zheng L, Lin N, Liang B, Huang H, et al. 2023. Prenatal diagnosis of non-mosaic sex chromosome abnormalities: a 10-year experience from a tertiary referral center. J Perinat Med 51: 904–912. doi:10.1515/jpm-2022-0552
      CrossRefMedlineGoogle Scholar
    221. ↵
      Xu R-H, Wei W, Krawczyk M, Wang W, Luo H, Flagg K, Yi S, Shi W, Quan Q, Li K, et al. 2017. Circulating tumour DNA methylation markers for diagnosis and prognosis of hepatocellular carcinoma. Nat Mater 16: 1155–1161. doi:10.1038/nmat4997
      CrossRefMedlineGoogle Scholar
    222. ↵
      Yang J, Ding X, Zhu W. 2018. Improving the calling of non-invasive prenatal testing on 13-/18-/21-trisomy by support vector machine discrimination. PLoS One 13: e0207840. doi:10.1371/journal.pone.0207840
      CrossRefMedlineGoogle Scholar
    223. ↵
      Yang X, Cai G-X, Han B-W, Guo Z-W, Wu Y-S, Lyu X, Huang L-M, Zhang Y-B, Li X, Ye G-L, et al. 2021. Association between the nucleosome footprint of plasma DNA and neoadjuvant chemotherapy response for breast cancer. NPJ Breast Cancer 7: 35. doi:10.1038/s41523-021-00237-5
      CrossRefMedlineGoogle Scholar
    224. ↵
      Yates LA, Aandahl Z, Richards SA, Brook BW. 2023. Cross validation for model selection: a review with examples from ecology. Ecol Monogr 93: e1557. doi:10.1002/ecm.1557
      CrossRefGoogle Scholar
    225. ↵
      Yi K, Ju YS. 2018. Patterns and mechanisms of structural variations in human cancer. Exp Mol Med 50: 1–11. doi:10.1038/s12276-018-0112-3
      CrossRefMedlineGoogle Scholar
    226. ↵
      Ying X. 2019. An overview of overfitting and its solutions. J Phys Conf Ser 1168: 022022. doi:10.1088/1742-6596/1168/2/022022
      CrossRefGoogle Scholar
    227. ↵
      Yoo S-K, Lim BC, Byeun J, Hwang H, Kim KJ, Hwang YS, Lee J, Park JS, Lee Y-S, Namkung J, et al. 2015. Noninvasive prenatal diagnosis of Duchenne muscular dystrophy: comprehensive genetic diagnosis in carrier, proband, and fetus. Clin Chem 61: 829–837. doi:10.1373/clinchem.2014.236380
      Abstract/FREE Full Text
    228. ↵
      Yu SCY, Jiang P, Choy KW, Chan KCA, Won H-S, Leung WC, Lau ET, Tang MHY, Leung TY, Lo YMD, et al. 2013. Noninvasive prenatal molecular karyotyping from maternal plasma. PLoS One 8: e60968. doi:10.1371/journal.pone.0060968
      CrossRefMedlineGoogle Scholar
    229. ↵
      Yu SCY, Chan KCA, Zheng YWL, Jiang P, Liao GJW, Sun H, Akolekar R, Leung TY, Go ATJI, van Vugt JMG, et al. 2014. Size-based molecular diagnostics using plasma DNA for noninvasive prenatal testing. Proc Natl Acad Sci 111: 8583–8588. doi:10.1073/pnas.1406103111
      Abstract/FREE Full Text
    230. ↵
      Yu SCY, Jiang P, Chan KCA, Faas BHW, Choy KW, Leung WC, Leung TY, Lo YMD, Chiu RWK. 2017. Combined count- and size-based analysis of maternal plasma DNA for noninvasive prenatal detection of fetal subchromosomal aberrations facilitates elucidation of the fetal and/or maternal origin of the aberrations. Clin Chem 63: 495–502. doi:10.1373/clinchem.2016.254813
      Abstract/FREE Full Text
    231. ↵
      Yu SCY, Jiang P, Peng W, Cheng SH, Cheung YTT, Tse OYO, Shang H, Poon LC, Leung TY, Chan KCA, et al. 2021. Single-molecule sequencing reveals a large population of long cell-free DNA molecules in maternal plasma. Proc Natl Acad Sci 118: e2114937118. doi:10.1073/pnas.2114937118
      Abstract/FREE Full Text
    232. ↵
      Yu SCY, Choy LYL, Lo YMD. 2023a. ‘Longing’ for the next generation of liquid biopsy: the diagnostic potential of long cell-free DNA in oncology and prenatal testing. Mol Diagn Ther 27: 563–571. doi:10.1007/s40291-023-00661-2
      CrossRefMedlineGoogle Scholar
    233. ↵
      Yu SCY, Deng J, Qiao R, Cheng SH, Peng W, Lau SL, Choy LYL, Leung TY, Wong J, Wong VW-S, et al. 2023b. Comparison of single molecule, real-time sequencing and nanopore sequencing for analysis of the size, end-motif, and tissue-of-origin of long cell-free DNA in plasma. Clin Chem 69: 168–179. doi:10.1093/clinchem/hvac180
      CrossRefMedlineGoogle Scholar
    234. ↵
      Zhao J, Wang T, Yatskar M, Ordonez V, Chang K-W. 2017. Men also like shopping: reducing gender bias amplification using corpus-level constraints. In Proceedings of the 2017 conference on empirical methods in natural language processing (ed. Palmer M, et al.), pp. 2979–2989. Association for Computational Linguistics, Copenhagen.
      Google Scholar
    235. ↵
      Zheng YWL, Chan KCA, Sun H, Jiang P, Su X, Chen EZ, Lun FMF, Hung ECW, Lee V, Wong J, et al. 2012. Nonhematopoietically derived DNA is shorter than hematopoietically derived DNA in plasma: a transplantation model. Clin Chem 58: 549–558. doi:10.1373/clinchem.2011.169318
      Abstract/FREE Full Text
    236. ↵
      Zhou Q, Kang G, Jiang P, Qiao R, Lam WKJ, Yu SCY, Ma M-JL, Ji L, Cheng SH, Gai W, et al. 2022. Epigenetic analysis of cell-free DNA by fragmentomic profiling. Proc Natl Acad Sci 119: e2209852119. doi:10.1073/pnas.2209852119
      CrossRefMedlineGoogle Scholar
    237. ↵
      Zhou Z, Ma M-JL, Chan RWY, Lam WKJ, Peng W, Gai W, Hu X, Ding SC, Ji L, Zhou Q, et al. 2023. Fragmentation landscape of cell-free DNA revealed by deconvolutional analysis of end motifs. Proc Natl Acad Sci 120: e2220982120. doi:10.1073/pnas.2220982120
      CrossRefMedlineGoogle Scholar
    238. ↵
      Zou H, Hastie T. 2005. Regularization and variable selection via the elastic net. J R Stat Soc Ser B Stat Methodol 67: 301–320. doi:10.1111/j.1467-9868.2005.00503.x
      CrossRefMedlineGoogle Scholar
    | Table of Contents
    OPEN ACCESS ARTICLE

    This Article

    1. doi: 10.1101/gr.278413.123 Genome Res. 35: 1-19 © 2025 Tsui et al.; Published by Cold Spring Harbor Laboratory Press

    Article Category

    ORCID

    1. Profile for Jiang, P.http://orcid.org/0000-0003-4523-3476

    Share

    Preprint Server



    Navigate This Article

    Current Issue

    1. January 2026, 36 (1)
    1. Current Issue
    1. Alert me to new issues of Genome Research