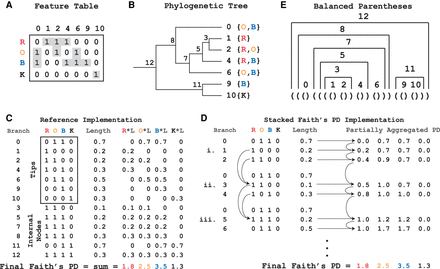
Partially aggregating branch lengths reduces the space complexity of the algorithm. (A) Faith's PD calculation depends on the representation of features present in samples. In the table, the letters (R, O, B, K) represent samples and the numbers (0, 1, 2, 4, 6, 9, 10) represent features. A “1” in an entry indicates the presence of a feature in the sample. SFPhD uses sparse table data structures, which reduce memory by only keeping track of the nonzero values in a matrix (highlighted in gray). (B) A mock reference phylogenetic tree is shown, with the features from A as tips. Labels for the samples from A are located next to tips that they contain. The nodes are labeled by their order in a postorder traversal of the tree. (C) Graphic depiction of the reference implementation's calculation of Faith's PD by first aggregating the presence/absence information for each branch in the tree, followed by multiplication by the branch lengths to get the metric constituents, and finally a sum over the entire branch × metric constituent table. (D) Graphic representation of the execution of SFPhD. On the left, the stack of presence/absence information is shown at three points during the algorithm's execution (i, ii, iii). Each of these times shows the stack immediately before memory is freed. On the right, the state of the partially aggregated phylogenetic diversity (PD) is shown after each node is added to the stack. Each row represents the vector after a step in the algorithm. In practice, there is only one such vector. (E) The balanced parentheses’ representation for the phylogenetic tree from B.











