FIND: difFerential chromatin INteractions Detection using a spatial Poisson process

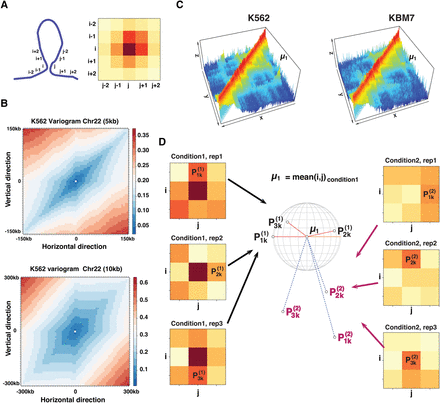
Existence of the spatial dependency and the idea behind our model. (A) Illustration of the spatial dependency along neighboring loci in the Hi-C contact map. (B) Semivariogram showing the directional variability between interaction bins separated by a certain horizontal and vertical distance in the Hi-C contact map. (C) A differential interaction can be considered as a change of the intensity around the 3D coordinate (i, j, f_ij) of a reference point μ₁. (D) Principle of the k-nearest neighbor (KNN) intensity estimation in a 3×3 window around a pairwise interaction (i, j). Given an interaction (i, j) with a mean frequency 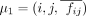in the first condition (represented by the mountain tip in C), if there is no structural change, we expect the interaction frequencies from the second condition to have a similar density around the point μ₁ in the 3D space. Thus, for each condition and each replicate, we calculate the 3D distance between each bin in the surrounding window and μ₁ and order them according to their distance. We note as the kth-nearest neighbor to the point μ₁ from the nth replicate of condition c ∈ {1, 2}. Then, we estimate the density of the KNNs around μ₁in the first condition 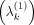and in the second condition . The density of the KNNs around μ₁ is expected to be stable between the two conditions. To decide if the change of the KNN density around μ₁ is significantly large or small, we use a Fisher distribution. The same principle applies if we use μ₂ (the mean in condition 2) as our reference point.