Ultrafast genome-wide scan for SNP–SNP interactions in common complex disease
Abstract
Long-range gene–gene interactions are biologically compelling models for disease genetics and can provide insights on relevant
mechanisms and pathways. Despite considerable effort, rigorous interaction mapping in humans has remained prohibitively difficult
due to computational and statistical limitations. We introduce a novel algorithmic approach to find long-range interactions
in common diseases using a standard two-locus test that contrasts the linkage disequilibrium between SNPs in cases and controls.
Our ultrafast method overcomes the computational burden of a genome × genome scan by using a novel randomization technique
that requires 10× to 100× fewer tests than a brute-force approach. By sampling small groups of cases and highlighting combinations
of alleles carried by all individuals in the group, this algorithm drastically trims the universe of combinations while simultaneously
guaranteeing that all statistically significant pairs are reported. Our implementation can comprehensively scan large data
sets (2K cases, 3K controls, 500K SNPs) to find all candidate pairwise interactions (LD-contrast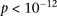 
) in a few hours—a task that typically took days or weeks to complete by methods running on equivalent desktop computers.
We applied our method to the Wellcome Trust bipolar disorder data and found a significant interaction between SNPs located
within genes encoding two calcium channel subunits: RYR2 on chr1q43 and CACNA2D4 on chr12p13 (LD-contrast test, 
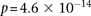). We replicated this pattern of interchromosomal LD between the genes in a separate bipolar data set from the GAIN project,
demonstrating an example of gene–gene interaction that plays a role in the largely uncharted genetic landscape of bipolar
disorder.
Genome-wide association studies (GWAS) have successfully identified hundreds of genetic markers associated with a wide range of diseases and quantitative traits (Hindorff et al. 2009; Manolio et al. 2009). Unfortunately, for most common diseases, nearly all associated variants have small effect sizes and taken together explain very little of the genetically heritable variation of the phenotype (Craddock 2007)—a phenomenon often posed as the conundrum of “missing heritability” (Maher 2008). Furthermore, single-locus association methods tend to implicate individual genes in a particular disease or trait, which in turn highlight a single biological entity involved (Saunders et al. 1993; Hugot et al. 2001; Neale et al. 2010). They do not, by definition, seek to implicate links between the functional elements of a system or elucidate pathway connections that may be broken. Investigation of joint gene–gene effects can therefore improve the explanatory ability of genetics twofold. Firstly, interaction—or statistical epistasis, as defined by Fisher (1918)—is hypothesized to explain a part of disease heritability (Marchini et al. 2005; Evans et al. 2006). Secondly, finding significant statistical links (epistatic or otherwise) between genes could provide strong indications of molecular-level interactions that differ between cases and controls.
However, an all-pairs (or all-triples) scan of SNPs genome-wide still poses widely discussed computational challenges due
to the sheer size of the combinatorial space (Marchini et al. 2005), both for data sets typed on genotyping arrays (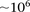
SNPs) and sequencing technologies (
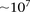SNVs). Some methods address this problem by restricting the analysis to a small subset of candidate markers—those identified
through single-locus analysis or those of biological interest (Emily et al. 2009), or by only checking for interactions between SNPs that are physically close to one another (Slavin et al. 2011). Others like EPIBLASTER (Kam-Thong et al. 2010) and SHIsisEPI (Hu et al. 2010) make use of specialized hardware like multiple Graphical Processing Units (GPUs) to finish computation on genome-wide data
sets on the order of days, rather than weeks or months. While it is known that reductionist, candidate SNP-based approaches
can miss many real interactions (Culverhouse et al. 2002; Evans et al. 2006) and fail to provide novel biological insights in an unbiased manner, brute-force approaches that rely on hardware for speedup
may also scale poorly as data sets increase in size and interaction tests increase in complexity.
For genome-wide interaction analysis to become pervasive, there is a pressing need for algorithmic insights that make interaction testing on large data sets a scalable proposition, without placing undue computing or hardware demands on the investigator. The contribution of our work is such a method. Recently, others had exploited the fact that contrasting the linkage disequilibrium (Zhao et al. 2006), Pearson correlation (Kam-Thong et al. 2010) and log-odds ratio (Plink “--fast-epistasis” option) between a pair of SNPs in cases and controls could be computed more efficiently than maximum likelihood estimates in a logistic regression. Usefully, these computationally efficient contrast tests showed high congruence with statistical epistasis under a variety of genetic models. In this study, we do not devise a new statistical test; rather, we use a simplified version of the LD-contrast test for interaction (Zhao et al. 2006) to demonstrate our computational principles. Our version seeks pairs of physically unlinked (often interchromosomal) SNPs that are in strong LD in cases, but in weak LD, no LD, or reverse LD in controls.2
Our computational approach is driven by the intuition that most genome-wide interaction methodologies only report SNP pairs that are statistically significant (as per the test used) after correcting for the number of tests. The question we ask is this: Given a statistical test, is it possible to identify all the significant SNP pairs with high probability (power), without actually applying the test to all possible combinations genome-wide? In other words, can we design a search algorithm that accepts an arbitrary significance cutoff (as input from the user), and then finds all SNP pairs that will pass this cutoff without a brute-force search? We show here that for some contrast tests, this is indeed possible. At this juncture, it is imperative that we point out the two distinct meanings of “power”: Here, unless otherwise specified, we mean the power of an algorithm to identify SNP pairs for which a test statistic is large (i.e., significant), whereas in the broader context of genome-wide interaction mapping literature, power is the ability of a statistical test to detect a real interaction in the data set. Our work focuses on addressing the computational issues that plague an exhaustive search for interaction, leaving issues of statistical power for a separate discussion.
The rest of this study is structured as follows. First, we briefly review a simple LD-contrast test that compares LD between binary allelic states (rather than 0/1/2 genotypes) in cases and controls. Next, we present a novel computational framework—probably approximately complete (PAC) testing—that quantifies the power of a search done by an algorithm. PAC is an intuitive concept: For example, a brute-force method that tests all-pairs of SNPs genome-wide is considered fully powered at finding all significant pairs in our framework (i.e., 100% probability of finding all pairs whose test statistic clears the significance cutoff) and have no element of approximation at all (i.e., 100% complete scan of the interaction space in the case-control data set). In this study, we design a two-stage PAC test for common complex diseases that is guaranteed to find all significant pairwise interactions with high power (e.g., probability >95% of finding all pairs with a significant statistic) by looking at almost the entire space of possibilities (e.g., ∼99% complete scan of interaction space). In return for accepting a small loss of certainty and power, we show that algorithms that offer tremendous computational gains can be designed. We evaluate the performance of our implementation of this framework (SIXPAC) on genome-scale data and then present the results of our analysis on bipolar disorder (BD) in the Wellcome Trust Case Control Consortium (WTCCC) data set (Craddock 2007).
Methods
Outline
The goal of our method is to efficiently identify the set of SNP pairs that have vastly different LD in cases and controls from the universe of pairs genome-wide—if any such pairs exist at all. First, we define the LD-contrast statistic and establish a minimum cutoff value that determines whether a pair of SNPs has a statistically significant contrast in a genome-wide study or not. Next, we devise a stage 1 filtering step that identifies potential case–control differences in LD by looking for LD in cases alone. We quantify the losses that stage 1 incurs (false negatives) by applying this “approximate” version of the full LD-contrast test.
In stage 2, the candidates shortlisted based on their LD in cases are tested using the full cases-versus-controls LD-contrast test and either validated or discarded based on the difference. Stage 2 is needed to distinguish stage 1 shortlisted candidates that are true interactions from false positives. False positives may include SNP pairs drawn by pure chance, and also pairs that show large LD in cases, but also show large LD in controls in the same direction. Such a systemic inflation of disequilibrium between alleles in cases and controls might be due to other factors like population stratification, technical artifacts, or ascertainment bias and is, by definition, not associated with phenotype.
The motivation for dividing the search into two stages is because the stage 1, case-only, “approximate” filtering step can be processed extremely rapidly by exploiting computer bitwise operations, making it much faster than a brute-force approach. We present the novel randomization technique called group-sampling with which we can efficiently find SNP pairs that are in strong LD in cases. However, like every randomization algorithm, we need to stop sampling when we are reasonably certain that all significant (high LD) candidates have already been encountered and shortlisted. Consequently, at the end of stage 1, we are left with a “probably complete” list of pairs that demonstrate severe LD in cases. Taken in conjunction, this design outputs a “probably approximately complete” (PAC) catalog of interacting SNP pairs at the end of the filtering stage, which are subsequently screened by the full test. We demonstrate that our software implementation of this PAC-testing framework can find approximately all significant SNP pairs in current GWAS data sets with arbitrarily high power (e.g., >99% probability) at a fraction of the computational cost of an exhaustive search.
Definitions and notation
For purposes of illustration, consider two binary matrices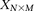 
and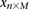 
, representing the cohorts of 
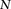haploid cases and 
haploid controls typed at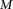 
polymorphic sites, respectively (we extend this to the diploid human case below). 
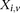denotes the allele carried by case 
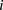at variant site 
(0 for major, 1 for minor), while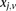 
similarly denotes the allele carried of control 
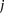at that site. Furthermore, we respectively denote 
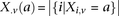and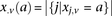 
as the number of cases and controls that carry allele 
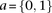at 
. Therefore,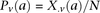 
and 
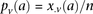are the corresponding allele 
-frequencies of 
in cases and controls. Since we are only discussing binary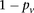 
carrier states 
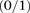, for ease of notation, we henceforth use 
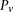instead of 
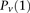, and (
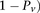instead of 
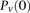(and analogously, 
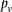and for controls).
We are interested in examining whether a haploid individual carries a certain combination of alleles at two (or more) sites.
Consider 
different binary sites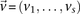 
, at which an individual can carry any one of 
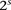unique allelic combinations. We say an individual carries allelic state 
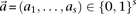at these sites if she carries allele 
at each one of the respective sites 
. Analogous to individual sites, we can also denote the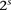 
different 
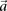-frequencies of 
by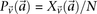 
in cases and 
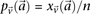in controls, where 
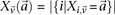and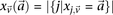 
are the number of 
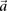carriers at 
in cases and controls, respectively. For example, if an individual carries 1-alleles (i.e., minor alleles) at each of the
sites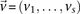 
, then we say she is a 
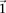-carrier of 
. The 
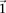-frequency of 
in cases (controls) is the fraction of cases (controls) that are 
-carriers of 
.
Binary representation of diploid genomes
For diploid genomes like humans, equivalent matrices of cohorts would be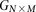 
for cases and 
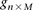for controls, where each entry 
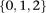in these matrices represents the number of minor alleles at the site, rather than the presence or absence of a minor allele.
Depending on the model of interaction the investigator is interested in, these may be transformed into an appropriate binary
representation in several ways. For our purpose, we represent each ternary genotype as two binary variables. The first variable
asks whether the individual carries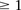 
copies of the minor allele (i.e., is dominant) at this SNP, while the second asks whether the individual carries exactly
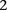copies of the minor allele (i.e., is recessive) at this SNP. In this format, cases and controls are represented by the binary
matrices 
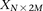and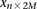 
, respectively, where each genotype 
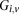is recoded as two binary values 
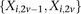for cases,
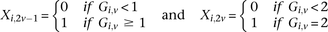and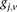 
is recoded equivalently as 
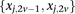for controls. For example, case #6 is represented as a recessive carrier of SNP #12 (variable coordinates: row 6, column
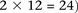by setting 
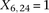. If case #6 is a dominant carrier of SNP #12, then we set both 
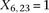and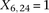 
. The notations for number of carriers and frequency of variables (and combination of variables) all follow analogously.
Statistical test for two-locus effect
We adapt the LD-contrast test for interaction between a pair of unlinked genotypes (Zhao et al. 2006) into a similar two-tailed test between a pair of unlinked binary variables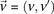 
,
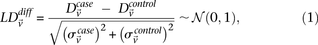where 
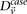and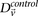 
represent the estimated LD between these variables in cases and controls, respectively, while 
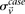and 
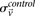represent the standard error of these estimators (see Supplemental Section 1 for derivation and details) and 
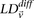is their LD contrast. This normalized statistic behaves as a Z-score, and for variable pairs that pass the significance cutoff in a genome-wide pairwise analysis (typically 
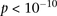or less on present day data sets), this statistic will assume large values (typically 6 or more).
Variable pairs with large differences in LD are of interest to several genetic models, and their signal can be dissected to reveal either statistical (epistatic) or biological interaction. Based on what is known about the genetic architecture of a specific disease, the relevant community of geneticists can bring different model assumptions to bear on a test for interaction. Here, we do not attempt to dictate a specific model that might cause such a difference in LD between the cases and controls. Rather, we focus on presenting a general method that can report all SNP pairs with a significant contrast and provide expert users with the flexibility to filter the results from such an analysis according to relevant assumptions. This can be done either a priori (e.g., removing SNPs with marginal signals before running a search for interaction), or a posteriori (e.g., discarding reported SNP pairs that do not provide evidence for statistical epistasis).
Two-stage testing design
A widely used simplification (Piegorsch et al. 1994; Yang et al. 1999; Cordell 2009) in genome-wide interaction scans is to divide the search effort into two stages: first filter candidates, and then verify
interaction. The crucial insight that permits this step is that we can expect physically unlinked markers to be in (or almost
in) linkage equilibrium in large outbred populations. Even for common diseases, the general population is mostly composed
of healthy controls (disease prevalence <50%). We show that in the absence of confounding factors like population stratification,
a pair of physically unlinked variables showing large LD contrast will be a pair that has large LD in cases rather than large
LD in controls. Without loss of generality, we focus our discussion on identifying pairs with strong positive LD in cases
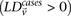. Pairs with strong negative LD between variables are easily modeled (with a trivial change in binary encoding) as strong
positive LD between the major allele at one and a minor allele at the other. Alternative variable pairings of this kind would
only require a different binary encoding scheme but introduce more confusing notation. A separate (but limiting) issue is
that of the statistical testing burden incurred by encoding alternate models, which we address in the Discussion.
A sequential two-stage testing strategy is designed as follows.
Stage 1 (shortlisting)
The stage 1 null hypothesis states that any pair of distal variables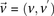 
should be in linkage equilibrium in cases.
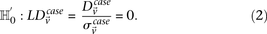
From Equation S1.1 (see Supplemental Section 1), we know that the distribution of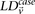 
is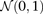 
. We shortlist only those variable pairs that reject the stage 1 null hypothesis at a significance level of 
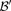. In other words, for a pair to be shortlisted as a candidate for follow-up, we require that the LD in cases between its variables
should exceed some threshold, i.e.,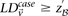 
. We determine this threshold to satisfy sensitivity/specificity constraints below.
Stage 2 (validating)
Next, we apply the LD-contrast test on candidates shortlisted by stage 1. This helps us to determine, for each candidate, whether the observed LD is indeed case-specific (and therefore a putative indicator of interaction) or pervasive in the population (and hence unrelated to disease). The stage 2 null hypothesis posits that there is no LD difference between cases and controls:
Putative significant pairs will reject this null hypothesis at a significance level of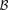 
(i.e., 
).
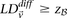To appreciate how such a two-stage design can capture almost all significant pairs in the data set and what the appropriate
significance cutoff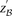 
in the stage 1 analysis must be, we now introduce the concept of a probably approximately complete search. A numerical example
depicting the concepts that follow is provided in Supplemental Section 9.
Probably approximately complete (PAC) search
Complete search
To find all significant variable pairs in the data set, current algorithms would sequentially visit each pair of SNPs, genome-wide,
and check whether each LD contrast exceeds the user-prescribed significance threshold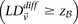 
by comparing cases and controls.
Approximately complete search
Here we ask, what threshold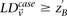 
can we apply in the filtering step, so as to capture almost all significant pairs by means of their disequilibrium in cases
alone? In other words, can most significant pairs (pairs for which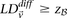 
) be captured without explicitly determining 
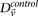at all? Furthermore, we wish to determine the proportion of significant pairs that such an approximation might miss. We show
that for most common diseases, an adequate cutoff for LD in cases is usually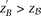 
(see Supplemental Section 2)—i.e. SNP-pairs with a severe LD-contrast (difference in LD between cases and controls) are usually
observable from their severe LD in cases alone.
Probably approximately complete (PAC) search
So far, our two-stage design has reduced the cumbersome task of counting the number of carriers for all variable pairs (genome-wide)
in cases and then again in controls, to the simpler task of shortlisting the small set of pairs that demonstrate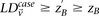 
. From a complexity standpoint, however, such a simplification (restricting the stage 1 analysis to cases only) does not change
the order or magnitude of the number of tests: This is still quadratic in the number of SNPs genome-wide. To address this
computational problem, we now introduce the novel randomization technique called “group sampling,” which can rapidly perform
the case-only shortlisting with arbitrarily high power, without explicitly checking all pairs of variables.
Group sampling
Rationale
From our observation that the LD statistic in cases is usually more severe than LD contrast (Supplemental Section 2), we deduce
that significant interacting pairs 
will show a minimum number of excess 
-carriers in cases: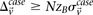 
. In a genome-wide analysis, as the universe of variable pairs tested grows, so does the burden of multiple test correction
that is applied to characterize statistical significance. Consequently, the number of excess of 
-carriers required in order for 
to achieve statistical significance in cases—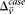
—grows commensurately. Group sampling overcomes the computational burden of a genome-wide analysis by using this “side effect”
of multiple-test correction to its advantage: The larger the number of variants typed, the larger is the universe of pairs
to be tested, and the larger the excess 
-carriers needed to make statistically significant pairs stand apart from the crowd. This observation allows us to quickly
prune the universe of pairs into a much smaller candidate set that is “guaranteed” to contain all significant pairs with arbitrarily
high probability.
For illustration purposes, let us consider a simplified version of the problem at hand. In this version, we are only interested
in searching through pairs of distal variables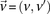 
, where both variables have 1-frequencies (
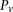and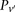 
) that lie within the narrow frequency window 
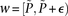. Let the set of all variables that lie within this frequency window be labeled 
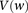. We wish to determine whether there exists a pair 
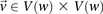, such that 
rejects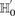 
. We can compute a lower bound on 
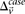for all such 
as:
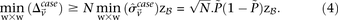
This is because the excess 
-carriers required for any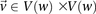 
to reject 
is at least as many as the excess 
-carriers required by the least frequent 
in that set: when 
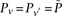. Therefore, the 
-frequency of all pairs that reject 
is at least: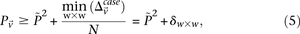
where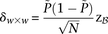 
is the minimum LD in cases for all significant pairs 
.
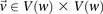Sampling a single group
Consider a group of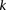 
cases drawn randomly (with replacement). If 
rejects 
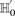, then the probability that all 
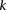cases in the group will be 
-carriers of 
has a lower bound 
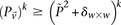. On the contrary, if 
does not reject 
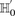, then the probability that such a group will contain all 
-carriers of 
purely by chance has an upper bound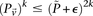 
—corresponding to the most frequent variable pair in 
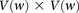. It is easy to see that if 
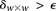, we are much more likely to observe a random group of cases that are all 
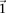-carriers of 
when it rejects 
.
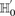The reason for drawing cases in groups (as opposed to one by one) is that it allows us to rapidly find the subset of variables
for which all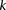 
cases are 
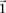-carriers. This is done with a native bitwise AND operation using computers, which is very fast in practice. In fact, the
larger the group size, the exponentially smaller the subset of variables carried by all cases in the group becomes. Furthermore,
long stretches of binary genotype data can be processed per CPU clock cycle, making this step even more attractive. Subsequent
to finding this small subset of variables, it is computationally efficient to enumerate all pairs (or indeed, triplets) among
them, and pass them on to stage 2.
Sampling multiple groups
If the group of cases we draw is sufficiently large (i.e.,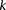 
is high), then it is extremely unlikely to contain only 
-carriers, not only when 
accepts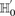 
, but also when this null is rejected because both 
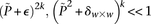. We can counter this by drawing up to 
independent groups (each containing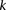 
random cases), so that the probabilities of not witnessing even a single group containing only 
-carriers decreases at diverging rates for the two realities:
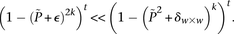
In fact, if 
does reject 
, then by varying the two parameters 
and 
the probability of observing at least one group of all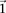 
-carriers can be driven arbitrarily high (type II error rate <
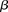) while keeping the probability of a chance observation relatively low (type I error rate <
). In other words, given fixed specificity and sensitivity constraints 
and 
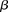(provided as input by the user), when 
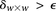, we can always find group-sampling parameter values 
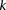and 
for which:
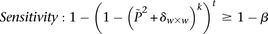
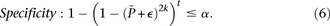
An illustration to visualize this technique is provided in Figure 1, while the simple algorithm implied by our toy problem logic is provided by Algorithm 1. The general formulation for PAC testing across all frequency windows (genome-wide) is described in Supplemental Section 4 and the logic provided by Algorithm 2.
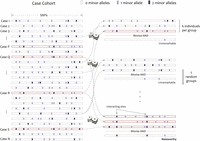
Group sampling. A cohort of 
cases is shown on the left, where the cases outlined in red—
, 
, 
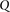, and 
—harbor an interacting pair of recessive variables. In other words, more cases carry the recessive–recessive combination than
would be expected by chance, given the marginal frequencies of each recessive allele. By repeatedly drawing random groups
of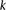 
cases (here 
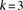), we are guaranteed to have drawn at least one group of individuals that carries both the variables in 
attempts with probability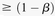 
. These variables (and others) are quickly determined by a bitwise-AND operation between the group of cases. Then, all pairs
of cocarried variables are enumerated and tested against the stage 1 null hypothesis (case-only analysis). Rejected combinations
are shortlisted and followed up in stage 2 (case vs. control analysis), where an interaction is identified.
Algorithm 1. Group sampling toy problem
Given all variables within frequency range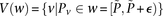 
Calculate significance threshold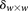 
Calculate sampling parameters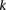 
and 
Repeat 
times:
Randomly choose a group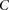 
of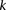 
cases (
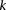rows from 
)
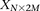Cocarried variables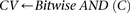 
For all unique combinations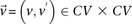 
:
If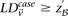 
do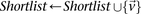 
Algorithm 2. Group sampling genome-wide (SIXPAC)
Assign all variables genome-wide to frequency windows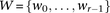 
For every pair of windows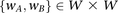 
:
Calculate significance threshold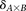 
Calculate sampling parameters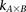 
and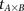 
Repeat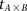 
times:
Randomly choose group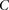 
of 
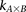cases
Cocarried variables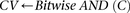 
Identify variables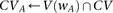 
Identify variables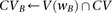 
For all unique combinations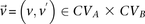 
:
If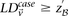 
do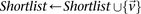 
For all shortlisted variables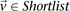 
:
If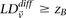 
output 
as an interaction
This concludes our discussion of a probably approximately complete search. PAC testing offers a powerful computational framework: As we shall demonstrate next, we can find approximately all significant SNP pairs genome-wide with high power in a fraction of the time that an exhaustive search would require.
Results
The major methodological contribution of this work is a novel randomization algorithm (group sampling), which can focus the computational effort toward finding significant pairwise interaction candidates, without testing all pairs genome-wide. To determine whether a candidate SNP pair is significant or not and to minimize the risk of false positives, in all our analyses, we subject the results to the most conservative threshold for significance in a genome-wide analysis—the Bonferroni corrected P-value of 0.05—unless otherwise stated. More sophisticated treatment of the multiple testing issues in interaction testing (e.g., Emily et al. 2009) is equally applicable and can be plugged into our method without violating any of the principles or assumptions. We also restrict our analysis to pairs of genetic markers (SNPs) only and choose to ignore gene–environment interactions for the moment. These simplifications serve to highlight the fundamental concepts of our approach, without loss of interpretable results. Our software implementation of this algorithm (SIXPAC) is available for download at http://www.cs.columbia.edu/∼snehitp/sixpac.
Data set
SIXPAC was used to analyze 1868 cases of the bipolar disorder (BD) cohort in the WTCCC against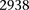 
combined controls from the 1958 British birth cohort (58C) and UK national blood service (NBS), all typed on the Affymetrix
5.0 platform, after cleaning all data as per requirement (Craddock 2007). Each of the remaining 455,566 SNPs remaining in the data set was encoded into two binary variables (dominant and recessive),
giving 911,132 binary variables genome-wide and a universe of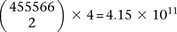 
potential variable pairs to be tested. Although we only report pairwise interactions that are significant at the Bonferroni
level in this data set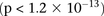 
, investigators who use less stringent multiple test correction can use SIXPAC to discover interactions at a different cutoff
as well.
To verify that the LD-contrast statistic follows a standard normal distribution, we drew random variable pairs genome-wide
and constructed a QQ plot. Like others before (Liu et al. 2011), we observed that WTCCC data cleaning was inadequate for interaction analysis and systematically applied more stringent
filters to preemptively screen out false positives that can be a result of bad genotype calls on a few individuals. Specifically,
81,085 additional SNPs that had <95% confidence calls (CHIAMO) in >1% of the individuals (cases and controls combined) were
removed. For the cleaned data set of 374,481 SNPs that remain, we verified that the LD-contrast statistic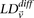 
for randomly drawn pairs of unlinked variables >5 cM apart was indeed a Z-score (QQ plots and additional cleaning details in Supplemental Section 5), in agreement with our null hypothesis.
Power analysis on spiked data
Next, we tested SIXPAC's computational sensitivity by searching for synthetic interactions inserted into the bipolar cases while keeping the joint controls unchanged. Eleven recessive–recessive interaction pairs between 22 SNPs on successive autosomal chromosomes (chr1 and chr2, chr3 and chr4, etc.) were simulated over a range of different parameters. Interactions between each pair of SNPs were simulated in a manner not to introduce a main effect, but effectively introduce only interaction effects. Details of this procedure are outlined in Supplemental Section 6.
Algorithm 2 configures the search parameters according to two user inputs: (1) a significance cutoff (LD-contrast test P-value), and (2) the minimum search power (defined as the power to discover all variable pairs that exceed the given significance cutoff, assuming such interactions exist). We tested SIXPAC on the synthetic data sets over a range of different input value combinations, to check whether we could discover the spiked interactions in accordance with theoretical estimates, and confirmed finding all of them at (or above) the power guaranteed to the user (Supplemental Section 7).
Computational savings from group sampling
To put the computational savings of our novel approach in context, we reviewed the literature for published, high-performance, genome-wide pairwise search methodologies that either (i) contrast a statistic for a pair of SNPs between cases and controls or (ii) directly test for statistical epistasis between a pair of SNPs using a regression model. Plink (Purcell et al. 2007) offers a --fast-epistasis option that tests pairs of SNPs using a statistic similar to ours: Specifically, it collapses each pair of SNPs completely into a 2×2 table of major versus minor allele counts, and subsequently contrasts the odds ratios of each combination between cases and controls. On the other hand, EPIBLASTER (Kam-Thong et al. 2010) operates on the entire 3×3 table of genotypes to contrast the exact Pearson's correlation of each SNP pair between cases and controls. Like Plink, SHEsisEPI (Hu et al. 2010) also contrasts odds-ratios of all SNP pairs reduced to a 2×2 table. Both EPIBLASTER and SHEsisEPI achieve speedup through the use of a GPU stack.
Among the methods that directly test for statistical epistasis, we report TEAM (Zhang et al. 2010a) and FastEpistasis (Schüpbach et al. 2010). The authors of FastCHI (Zhang et al. 2009), FastANOVA (Zhang et al. 2008), COE (Zhang et al. 2010b) and TEAM presented a review (Zhang et al. 2011) in which TEAM was reported as the most appropriate for handling human data sets, and was therefore chosen to represent the family of methods. TEAM achieves computational speedup by a novel approach that allows it to accurately identify interacting SNP pairs (for most statistical tests) by checking only a small subset of individuals in the cohort. Unlike EPIBLASTER, Plink --fast-epistasis, and SIXPAC, TEAM works directly on the logistic regression framework—giving it the ability to test a broader range of interaction models. The other method, FastEpistasis, reports epistasis in the analysis of quantitative traits (and is particularly built for gene-expression analysis) by implementing a rapid linear regression that takes advantage of multicore processor architectures. Notable among methods omitted in this comparison are Multifactor Dimensionality Reduction (Ritchie et al. 2001) and the Restricted Partition Method (Culverhouse et al. 2004), both of which partition the data according to genotypic effect in a relatively model agnostic manner. Consequently both methods test a variety of interaction models (alternate parameterizations) that are not currently captured by high-performance computational techniques like ours and others previously discussed. Another widely cited method, BEAM (Zhang and Liu 2007), does not scale to present day data sets (Cordell 2009) and was left out of this analysis. There are numerous other methods that perform whole-genome interaction scans (Emily et al. 2009; Zhang et al. 2009; Greene et al. 2010; Liu et al. 2011), including some that utilize sampling subsets of individuals for computational speedup (Achlioptas et al. 2011). An older review of a few of these is provided elsewhere (Cordell 2009).
Except for SIXPAC, all the time scales presented in Table 1 are performance figures as self-reported by the authors of each method (or in the case of TEAM, extrapolated from performance figures reported therein) on a data set of this size. Our synopsis does not constitute a comprehensive methods comparison and is presented solely to highlight the computational savings achieved by group sampling (Fig. 2). The reason SIXPAC is able to achieve its speedup without GPUs is because it does not need to exhaustively test all pairs of SNPs to identify the significant combinations.3 On the other hand, all other methods are burdened by a brute-force test of all pairs to identify such combinations. In confirmation of our estimates, they also report that genome-wide testing on ordinary CPUs requires several weeks of compute time (some report weeks even on a small cluster of computers). The application of group sampling was able to reduce this computational investment to ∼8 h.
Methods comparison
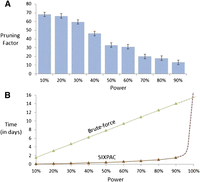
Computational efficiency. Our implementation of the two-stage PAC-testing framework (SIXPAC, orange line) was benchmarked on the cleaned WTCCC bipolar disorder data set (approximately 2K cases, 3K controls, 450K SNPs, four genetic models tested per distal SNP pair, 400 billion pairwise tests genome-wide). (A) The factor reduction in the universe of SNP pairs achieved by stage 1, for each power setting. Note that unlike brute force, this does not mean down-sampling the universe of SNP pairs, but rather involves reducing the probability of identifying any one of them. For example, a brute-force method would presumably test 40 billion pairs (and ignore the remaining 360 billion) to achieve 10% power on this data set. However, PAC testing scans all 400 billion pairs, but simply reduces the probability of finding the significant interactions among them to 10%. This results in shortlisting ∼68× fewer combinations through stage 1. (B) The efficiency of our software implementation of this method. We compare the performance of SIXPAC against the time taken by a brute-force approach of applying the LD-contrast test directly to all pairs (green line). All tests were benchmarked on a common desktop computer configuration (Intel i7 quad-core processor, 2.67 GHz with 8 GB RAM). The last data point shows the 90% power benchmarks, followed by dotted lines that illustrate how these estimates may continue as we approach 100% power. SIXPAC, like any randomization algorithm, will require infinite compute time to achieve 100% power but can approach very close at a small fraction of the brute-force cost. Lastly, we note that these measurements only reflect the performance of our Java program rather than what might be feasible with a different implementation of the algorithm.
Novel significant interaction in bipolar disorder
We ran SIXPAC on the BD data set with >95% power to check whether there exist any significant LD contrasts between pairs of
physically unlinked variables (SNPs >5 cM apart). We report the presence of only one statistically significant two-locus contrast
(BD cases vs. NBS+58C controls LD contrast,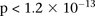 
) between SNPs lying within two calcium channel genes: rs10925490 within RYR2 on chr1q43, and rs2041140 and rs2041141 within CACNA2D4 on chr12p13.33. We successfully replicated the signal from this region at Bonferroni significance levels in a different bipolar
data set of Europeans (653 BARD cases, 1034 GRU controls) from the GAIN initiative (The GAIN Collaborative Research Group 2007; Smith et al. 2009) (also see http://www.genome.gov/19518664), which were typed on a different platform (Affymetrix 6.0). Deeper investigation revealed that the SNP in CACNA2D4 is 200 kb away from CACNA1C—a known calcium channel gene whose association to BD was only recently confirmed by combining large GWAS data sets for meta-analyses
(Ferreira et al. 2008; Sklar et al. 2008). Functional experiments have also confirmed the role played by genes at this locus in bipolar disorder (Perrier et al. 2011). Although channel ideopathies (and, more specifically, faults in calcium channels and signaling) have long been known to
play a major role in bipolar disorder, single-locus association methods were underpowered to implicate genes in these pathways
without considerably boosting their sample sizes (Craddock 2007; Ferreira et al. 2008; Sklar et al. 2008). Neither gene that we report—either at the known locus or novel locus—was identified as a candidate by the original WTCCC
analysis (Craddock 2007), which focused on effects visible to single-locus association.
Specifically, we found that the dominance variable of rs10925490 (one or more minor alleles) was in severe positive linkage
disequilibrium with the recessive variables of adjacent SNPs rs2041140 and rs2041141 (two minor alleles each) in BD cases,
and slight negative disequilibrium with them in controls, giving an LD-con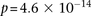trast 
. To verify that this signal was not due to any unaccounted biases, we first confirmed that high LD between the two variables
was specific to BD cases only, even when contrasted against samples from all other WTCCC disease phenotypes (six tests of
BD vs. other-disease-cases all show LD-contrast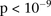 
). Next, we performed a permutation analysis to characterize the empirical distribution of the LD-contrasts statistic at the
theoretical significance level of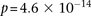 
(i.e., to check if 
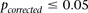). We ran SIXPAC on 100 phenotype permuted versions of the same data set (i.e., 100 whole-genome, all-pairs scans for interaction)
and observed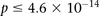 
between a pair of SNPs in only one such permutation (
).
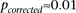Finally, we sought to replicate the observed difference in LD at these loci. In the GAIN data set, we considered all LD contrasts
in an area of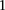 
SNP immediately upstream and downstream of rs10925490 in the dominant allelic mode, against 
SNP immediately upstream and downstream of rs2041140 in the recessive allelic mode. In other words, we tested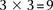 
pairs (around and including the original interaction), to test if any pair in this area bore an LD contrast that passed the
conservative Bonferroni significance cutoff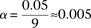 
. This roughly translates to a region 
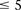kb upstream and downstream of each SNP in the original pair. Although there was no appreciable difference in LD between the
same SNPs (rs2041140/rs10925490 shows LD-contrast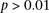 
), we observed a significant LD contrast 
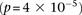between rs2041140 and rs677730 (the SNP immediately upstream of rs10925490 on the Affymetrix 6.0 platform). To confirm that
this observation was not likely by chance, we randomly picked 5000 pairs of physically unlinked (>5 cM apart) SNPs genome-wide
and tested an equal neighborhood of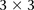 
LD contrasts around each pair in the GAIN data set. Only one out of 5000 random areas contained a SNP pair with a more significant
LD contrast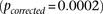 
.
To get a better picture of the LD-contrast landscape between SNPs in this region, we conducted a wider survey of the area
spanning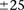 
SNPs (upstream, downstream, and including both rs2041140 and rs10925490) 
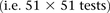. The scan reveals several additional pairs of SNPs that show differences in LD going in the same direction (strong LD in
cases, weak negative LD in controls), arranged in a strikingly similar pattern in both data sets, presenting strong evidence
of an interlocus effect. The two-dimensional LD-contrast spectrum for this larger area is presented in Figure 3, alongside the Manhattan plots for marginal association at each locus. The top SNP pair in the area (rs677730, d × rs11062012,
r) had LD-contrast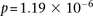 
in GAIN: A similar phenotype permutation analysis as earlier reveals that only 19 out of the 5000 randomly chosen 
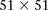areas genome-wide contained a more significant pair 
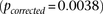. It can also be seen that there is no marginally significant association at these loci in either data set. Table 2 and Table 3 present a summary of these results.
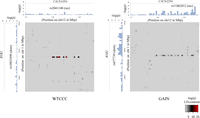
Bipolar disorder interaction. In a genome-wide scan of all 400 billion variable pairs (four genetic models tested per SNP
pair) in the WTCCC bipolar disorder data set (Affymetrix 500K), SIXPAC found one significant interaction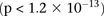 
between SNPs >5 cM apart that satisfied all our filtering criteria. The SNPs rs10925490 and rs2041140 lie within the RYR2 gene on chr1q43 and the CACNA2D4 gene on chr12p13.33, respectively. Each figure shows the −log(P-value) from a standard single-locus association test (allelic model) of the two SNPs as well as 25 SNPs immediately upstream
and downstream from each of them, along the x-axis and y-axis. Also shown in the grayscale area is the −log(p) from the pairwise LD-contrast test of all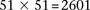 
variable pairs. As suggested by the original finding, SNPs around rs10925490 were considered in dominant allelic mode, while
SNPs around rs2041140 were in recessive mode. We replicated this signal by similarly testing 
dominant–recessive pairs of variables around the very same SNPs in a much smaller bipolar disorder data set from the GAIN
Consortium (Affymetrix 6.0). In the replication data set, we observe several pairs that cross the significance threshold and
a strikingly similar visual pattern in the LD-contrast landscape (see main text for a permutation analysis). The top pair
(rs677730–rs11062012) in this area is pinpointed with dashed lines (see main text for permutation analysis). Standard single-locus
association analysis does not yield any significant result in either data set, as seen in the marginal Manhattan plots (the
gray dashed line represents the genome-wide significance level).
Bipolar disorder interaction
BD interaction carrier counts of WTCCC cases and controls
Discussion
In this study, we introduced a novel method that defuses the computational challenge of a genome × genome interaction scan by using the statistical constraint toward, rather than against, our goal. Focusing only on interactions that have a chance of achieving statistically significant association, we developed a rapid filter that does not require the naive arduous scan of all pairs of variants. To demonstrate its utility, we implemented an established test for interaction that contrasts LD between cases and controls, to demonstrate how an exhaustive genome-wide multilocus association search is possible while saving an order of magnitude or more in computational resources. Usefully, we are also able to provide performance guarantees and quantify the approximate nature of our output, and our algorithm brings genome-wide three-locus scans into the realm of feasibility.
While the focus of this contribution is computational methodology, we prove applicability in practice to a classical GWAS data set. Among widely investigated common diseases, bipolar disorder remains one of the most recalcitrant phenotypes to GWAS methodology (Craddock and Sklar 2009), perhaps in part because of the limitations of single-locus association analysis. We highlight the power and utility of multilocus effects in terms of uncovering molecular processes by exposing two calcium channel–coding genes as affecting bipolar disorder, supporting recent discoveries that were only made possible through a significant increase in data set size. We have replicated this observation in an independent data set, strongly suggesting a bona fide underlying interaction between members of a gene family known to be functionally associated with bipolar disorder, making it suitable for further investigation.
Compared to the number of single-locus associations, GWAS of common phenotypes in humans have uncovered very few reproducible gene–gene effects so far. This is partly because interaction analyses for human populations are difficult to design and interpret (Cordell 2002; Phillips 2008). A conventional test for statistical epistasis is expected to only identify loci whose combined effect on phenotype is not explained by the addition of their individual effects, for an appropriately chosen scale. In case–control studies, this typically involves applying a logistic regression to check for significance of the interaction term(s) after accounting for main effects (Wang et al. 2010), which is equivalent to a test for deviation from multiplicative odds (or additive log-odds). However, there are several limitations to this approach—scale of choice (Mani et al. 2008), assumption of a genetic model by which two loci combine their effects (Hallander and Waldmann 2007), limited models of interaction that can be tested (Li and Reich 1999; Hallgrímsdóttir and Yuster 2008), and limited sensitivity of logistic regression to non-normal residuals, among others. How these factors might cumulatively affect a test for other models of genetic interaction has not yet been decisively established.
Furthermore, true biological interaction between two or more loci may or may not manifest itself as a departure from additivity. Two loci whose main effects appear to combine in an additive manner might also indicate their biological co-involvement (and hence “interaction”) underlying the disease (Wang et al. 2011). In general, two-locus association tests are known to contribute signal independently from what is seen by conventional single-locus association tests (Marchini et al. 2005; Kim et al. 2010), and comprehensive multilocus association strategies may be worth undertaking despite the increased multiple testing burden (Evans et al. 2006). Indeed, recent work (Zuk et al. 2012) showing that alternative models of biological interaction could confound estimates of heritability has redirected the attention of the genetics community to the potential of interaction studies.
A previous genome-wide scan for statistical epistasis on the same bipolar disorder data set had reported Bonferroni significant
epistasis between rs10124883 and four other SNPs (Hu et al. 2010). As expected, all four pairs approached (but did not clear) Bonferroni significance levels as per the LD-contrast test as
well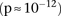 
—and could therefore be captured simply by lowering the significance cutoff. This congruence between tests for statistical
epistasis and contrast tests has been exploited by others (Plink, EPIBLASTER) and, indeed, also holds for the binary LD-contrast
test (see tables in Supplemental Section 6). But whereas other methods would use a brute-force testing strategy to identify
candidate SNP pairs, PAC testing will accomplish the same result much quicker by looking at a small fraction of the pairs.
Our findings do suggest that unlike stepwise regression approaches that sequentially attribute residual variance/deviance
to each of their components, tests that make fewer assumptions regarding scale may, indeed, be more powerful at capturing
a wider range of interactions. Conversely, a distinct advantage of regression over our LD-contrast test remains its clear
interpretation and measurement of effect size; although the difference in LD between cases and controls is consistent and
reproducible across data sets, it does not immediately suggest a clear causal genetic model underlying this signal. We dissected
this interaction using the standard logistic regression,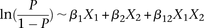 
, where 
codes for dominance carrier status at rs10925490 while 
codes for recessive carrier status at rs2041140. The main effects 
were observed to be not significant, while the epistasis term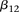 
was considerable (
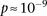), suggesting deviation from multiplicative odds is one option. We also considered the standard full genotype model (0/1/2
parameterization of predictor variables) with 8 degrees of freedom (Cordell and Clayton 2002) as implemented by INTERSNP (Herold et al. 2009), where the most significant test (Test 6, 
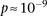) was the one comparing the full model against a model that accounts for just within-SNP additive and dominance effects. In
a genome-wide search for interaction using logistic regression, these levels are likely to fall short of significance cutoffs
after correcting for hundreds of billions of tests performed, which explains why other methods seeking statistical epistasis
on the same BD data set did not report LD between the RYR2-CACNA2D4 as a significant finding. A true etiological understanding of this persistent difference in LD may require sequencing at
each locus to identify the interacting variants.
Limitations and extensions
The major contribution of this work is a computational technique to rapidly identify SNP pairs with large values of a test statistic without performing a brute-force search. While we assessed the issue of power with regard to our randomization algorithm, we left the separate (but equally important) concept of statistical power unaddressed—i.e., the ability of an interaction test to spot a true biological interaction in the data set. Although contrasting LD, correlation, and odds-ratios between cases and controls have all separately been characterized as powerful tests for interaction, each test makes specific model assumptions and is powerful only under its own regime. Consequently, the absence of interaction reported by SIXPAC (or, indeed, by any other software) does not imply the absence of interaction itself, but could simply mean lack of statistical power of the test, inadequate number of samples, or, simply, incorrect model assumptions. During the course of publishing this method, minor corrections were suggested for a range of contrast statistics to improve their power and decrease type I error rate (Ueki and Cordell 2012). Again, we note that modifications to these tests can be easily adopted into our computational methods—which are agnostic of statistics.
In contrast to the performance gains offered by group sampling are its two notable weaknesses. First—like any other randomization algorithm—group sampling can never achieve 100% power (probability of completion), whereas brute-force approaches will. Second, by virtue of limiting itself to binary features, testing for genetic models that incorporate allelic dosage and trend effects using group sampling does not appear straightforward. Although extending our computational principles to implement rapid correlation and odds-ratio contrast tests (among others) may be appealing, the loss of statistical power from increasing the number of tests is less easily addressed. Where we currently encode recessive and dominance binary status, each additional test may require a different encoding of features (genotypes, or combinations thereof), thereby adding to the multiple testing burden. Overcoming these limitations appears nontrivial, and increases in sample size will almost certainly play a crucial role in discovering these hidden genetic connections.
Extrapolating from the hardware speedups reported by others (Hu et al. 2010; Kam-Thong et al. 2010) may suggest that a high-performance GPU-enabled implementation of our method might offer a scan of all-pairwise interactions in a few minutes, and all three-way interactions on the order of a day(s) in large GWAS data sets. But a more immediate concern related to testing three-way interactions would be the statistical power and semantic interpretation of such a test (conceivably devised on a 2×2×2 binary table). In conclusion, we note that while the transition of association studies from SNP arrays to full ascertainment of variants may have led to analytical emphasis on rarer alleles, it has only increased the impetus to examine the spectrum of multilocus effects. With so many more variants to consider, the computational limitations will only become more severe, but the solutions reported will be ever more essential.
Acknowledgments
We are grateful to all patients who contributed data to both of the bipolar disorder cohorts used by our work. We thank the Wellcome Trust Case Control Consortium (http://www.wtccc.co.uk) and the Genetic Association Information Network (GAIN) initiative (http://www.genome.gov/19518664) for making their data publicly available to us through the database of genotypes and phenotypes (dbGaP), as well as their funding bodies, the Wellcome Trust and the National Institutes of Health. This work was funded in part by the Microsoft Research PhD Fellowship awarded to S.P., and NSF awards 0829882 and 0845677 and NIH grant U54 CA121852-06 awarded to I.P.
Footnotes
-
↵1 Corresponding author
E-mail itsik{at}cs.columbia.edu
-
↵2 Disequilibrium between physically unlinked loci is also often called Gametic Phase Disequilibrium (Wang et al. 2010), but for purposes of this study, we consider both terms equivalent—in particular, we do not imply physical linkage/proximity on the genome with the term LD.
-
↵3 However, we report that the SIXPAC implementation currently takes advantage of multicore CPU architectures with large reserves of RAM to speed up computation, as well as cluster computing infrastructures to distribute computational burden across multiple nodes—all with little or no effort on the part of the end user. Details are provided on the software web page.
-
[Supplemental material is available for this article.]
-
Article published online before print. Article, supplemental material, and publication date are at http://www.genome.org/cgi/doi/10.1101/gr.137885.112.
- Received January 29, 2012.
- Accepted July 3, 2012.
This article is distributed exclusively by Cold Spring Harbor Laboratory Press for the first six months after the full-issue publication date (see http://genome.cshlp.org/site/misc/terms.xhtml). After six months, it is available under a Creative Commons License (Attribution-NonCommercial 3.0 Unported License), as described at http://creativecommons.org/licenses/by-nc/3.0/.
