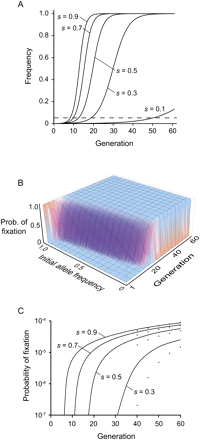
Population genetic analysis of the fixation of new mutations under positive selection and complete self-fertilization. (A) Deterministic sweep of a new adaptive mutation in an infinitely large self-fertilizing population under different strengths of selection. There can be a significant lag before the mutation reaches a high enough frequency to be detectable at the sensitivity threshold present in this experiment (dashed line). (B) Solution to the diffusion equation for finding the probability of fixation of a segregating allele (s = 0.5, Ne = 1000). The probability of fixation for a new mutation over the course of the experiment is calculated by summing over the cumulative probability of fixation for an initial allele frequency of 1/2000. (C) Cumulative probability of fixation over a given number of generations for varying levels of positive selection. Solid lines show simulation results that simultaneously include mutation, drift, and selection (Ne = 1000; μ = 2.6 × 10−9). Points below each line show the results of the diffusion approximation in which mutation is treated separately from drift and selection. The diffusion approximation tends to underestimate the probability of fixation, especially during early generations and under weaker selection.











