Testing the Parsimony Test of Genome Duplications: A Counterexample

Whereas the role of genome duplication(s) in yeast and plants has been widely accepted, the hypothesis of genome duplication in early vertebrates (Ohno 1970) is still under controversy (Wolfe 2001). According to the current version, the 2R model, there were two rounds of polyploidization: one occurring before the divergence of jawless vertebrates and the other just after (Sidow 1996). Recently, doubt has been raised about the 2R model because the evidence was found to be weaker than previously thought (Wolfe 2001). For the proponents of the 2R model, this doubt may be explained as a combination of rapid gene deletion, sequence diversity, and chromosome rearrangement (Nadeau and Sankoff 1997; Wang and Gu 2000). For the opponents, however, the lack of strong evidence is sufficient to refute the 2R model, applying “Ockham's Razor” (Hughes et al. 2001; Makalowski 2001).

Alternatively, the model of small-scale tandem duplications (TDs) followed by translocations was invoked (Hughes et al. 2001). Moreover,Hughes et al. (2001) used the parsimony to test whether the TD hypothesis is “better” than the 2R hypothesis. The basic procedure is to infer the minimum number (G) of genetic events to explain the gene's current distribution on human chromosomes under each competing model. Here the genetic events include gene duplications (D), losses (L), and translocations (T), that is,G_M  = D + L + T, where the subscript M = 2R for the 2R model orTD for the TD model. Under this parsimony, the TD hypothesis is favored if G_TD < G_2R ; otherwise, the 2R model is favored. After examining 20 vertebrate gene families,Hughes et al. (2001) showed that in 14 cases the TD hypothesis was more parsimonious than the 2R hypothesis.

It should be noted that any test based on parsimony has assumptions.Hughes et al.'s test (2001) is valid only if these genetic events, that is, gene duplication, loss, and translocation, occurred at approximately the same evolutionary rate. If so, a smallerG_M value between the 2R and TD models reflects which model is more likely to be true. Without reliable data, however, it is difficult to test whether this assumption holds.

Instead, we adopt the testing-data approach, that is, use genome sequence data in which genome duplication(s) is almost uncontested. We found that the Arabidopsis genome is suitable for this purpose (The Arabidopsis Genome Initiative 2000; Blanc et al. 2000).

Vision et al. (2000) conducted a genome-wide search, resulting in 103 paralog blocks (http://www.igd.cornell.edu/∼tvision.arab). One paralog block has two copies that are located in different chromosomal regions. A duplicate gene pair appears in both copies, whereas a singleton gene appears only in one of them. For most paralog blocks, the number of singleton genes (S) is much larger than that of duplicate pairs (x). Let n = S + xbe the total number of predicted ancestral genes (Vision et al. 2000). Thus, the retention frequency q = x/nprovides an estimate for the survival rate of both duplicate genes in a paralog block.

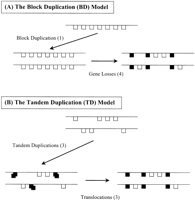
Under the model of block duplication (BD), the paralog block was generated by the segmental duplication of one chromosome. Single genes within the paralog block are the consequence of gene deletion (Fig.1A). Some of them may be translocated from other regions (after duplication), but the count would not be affected. Apparently, the total number of genetic events of a block is G_BD  = (1-q)n + 1, that is, the total number of gene losses, (1-q) n, plus one-time BD.

View larger version:

• In this window
• In a new window

• Download as PowerPoint Slide

Figure 1.

(A) The block duplication (BD) model. Assume (ancestral) seven genes in a chromosome region. After one BD (D = 1), four duplicate genes are lost (L = 4). In this case, no translocation (T  = 0). Thus, the total number of genetic events is G = 1 + 4 + 0 = 5. (B) The tandem duplication (TD) model. There are two chromosome regions with four and three genes, respectively. After three TDs (D = 3), one copy in each duplicate pair is moved to another chromosome by translocation (T =3), and no gene loss (L = 0). The total number of genetic events is G = 3 + 0 + 3 = 6.

Under the model of TD (TD), gene pairs in the paralog blocks were generated via TDs followed by translocations (Fig.1 panel B). Because there are qn gene pairs, each of which has two events, the total number of genetic events isG_TD  = 2qn. Then, the parsimony test uses the difference to test which one is more parsimonious: δ  > 0 favors TDs, and δ  < 0 favors BD. The sampling variance of δ is given by Var(δ) =  9n²Var(q), whereVar(q) = q(1-q)/n under the binomial distribution. The statistical significance of rejecting the null hypothesis δ  = 0 (G_BD  =  G_TD ) is assessed approximately by the standard z-test.

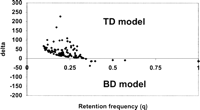
We have computed q and δ for 103 paralog blocks (Fig.2). Surprisingly, the majority (94) of paralog blocks have δ > 0, indicating that the TDmodel is favored. For instance, block 10 has two homologous regions located in chromosomes 1 and 2, respectively (Vision et al. 2000). There are 254 ancestral genes, among which 52 are paired, resulting inq = 0.205, δ = 99 and z = 5.13 (p < 0.01). In total, 68 paralog blocks show δ > 0 significantly, whereas two blocks show δ < 0 significantly (p < 0.05, z-test).

View larger version:

• In this window
• In a new window

• Download as PowerPoint Slide

Figure 2.

The δ value is plotted against the retention frequency (q) for 103 blocks. δ > 0 means that the TD model is favored, and δ < 0 means that the BD model is favored.

If all 103 duplicated blocks are the result of m-round genome duplications, the sum of genetic events is m duplication events plus the sum of gene losses over 103 blocks, that is,G_R  = m + Σ_i(1-q_i )n_i, where q_i andn_i are the retention frequency and the number of ancestral genes in block i, respectively. Note that mranges from 1 (The Arabidopsis Genome Initiative 2000) to 5 (Vision et al. 2000). Because under the TD model, the total number of genetic events (duplication + translocation) over all blocks is Σ_i 2q_i n_i , the difference (G_R -G_TD ) turns out to be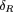 and the sampling variance Var(δ_R) =  9Σ_i n_i ²Var(q_i ). From Vision et al. (2000), we obtained Σ_i n_i  = 11847, and Σ_i q_i n_i  = 2794, resulting in δ_R = 3465 + m andVar(δ_R) = 151.84. Thus, for m = 1–5,z = 281.3–281.6, which means δ_R > 0 highly significantly (p < 10^–5), and the TD model is strongly favored.

In summary, when the parsimony test of Hughes et al (2001) is applied for the Arabidopsis genome sequence data, the TD model is statistically superior to the BD model or the genome duplication model. However, this inference is contrasted with substantial evidence supporting the genome (block) duplication(s) in theArabidopsis (Vision et al. 2000). This dilemma is probably due to the fast rate of gene loss after gene (genome) duplication (note that the mean of q is 0.23). In the yeast, only ∼ 15% duplicate pairs maintained after the genome duplication (Wolfe 2001).

Some theoretical models predict that the rate of gene loss should be at least an order of magnitude higher than the rate that both duplicates survive (Ohta 1988; Walsh 1995). In addition, the blocks with δ < 0 (BD favored) are generally those with the highest retention frequency (Fig.2).

We conclude that the evolutionary trajectory of gene duplication, loss, and translocation may not follow the parsimony principle formulated byHughes et al. (2001). Therefore, the potential misleading should be fully recognized when the parsimony test (Hughes et al 2001) is used for testing the 2R model in vertebrates. Of course, the parsimony test is only one of anti-2R arguments in Hughes et al. (2001), so the debate is not over yet.